The graph of \(f(x) = x^2\) is the same as the graph of \(y = x^2\) Writing graphs as functions in the form \(f(x)\) is useful when applying translations and reflections to graphs Translations · The point of the vertex is (1,2) The sign of a is positive, therefore, the parabola has a minimum Substitute x=0 into the equation to find yintercept You know that this point is (0,3) Know that the parabola has a minimum, the vertex and the yintercept, you can graph it as you can see in the image attached125x3 − 150x2 60x − 8 View solution steps Solution Steps f ( x ) = ( 5 x 2 ) ^ { 3 } f ( x) = ( 5 x − 2) 3 Use binomial theorem \left (ab\right)^ {3}=a^ {3}3a^ {2}b3ab^ {2}b^ {3} to expand \left (5x2\right)^ {3} Use binomial theorem ( a − b) 3 = a 3 − 3 a 2 b 3 a b 2 − b 3 to expand ( 5 x − 2) 3 125x^ {3}150x^ {2

Graphing Square And Cube Root Functions Video Khan Academy
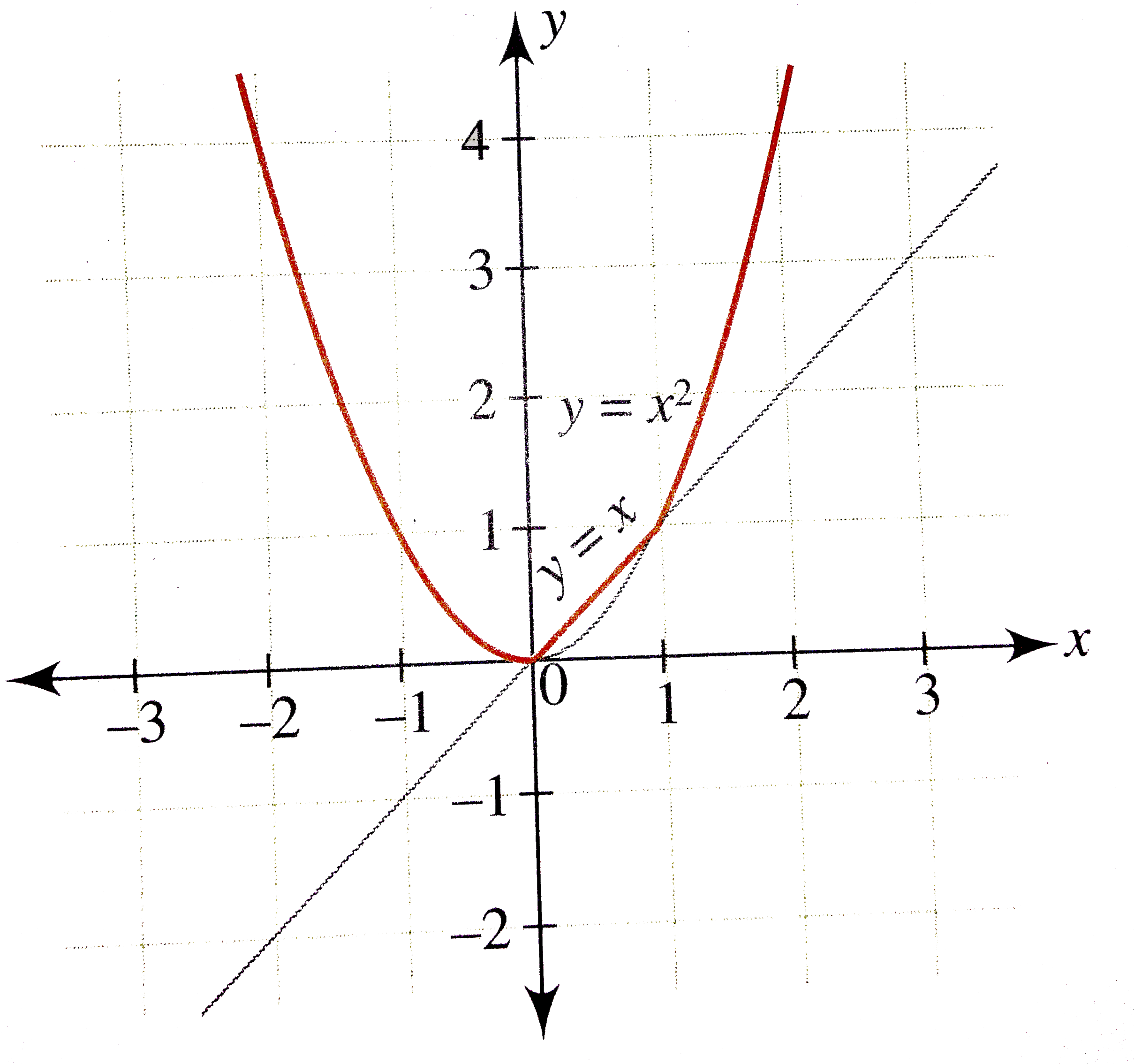
F(x y)=3-x^2-y^2 graph
F(x y)=3-x^2-y^2 graph-The graph of f (x)=2/3x2 represents a graph of a linear function On the given graph you can find all of the important points for function f (x)=2/3x2Steps Using Derivative Rule for Sum f ( x ) = 3 x ^ { 2 } 1 f ( x) = 3 x 2 1 The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of ax^ {n} is nax^ {n1} The derivative of a polynomial is the sum of
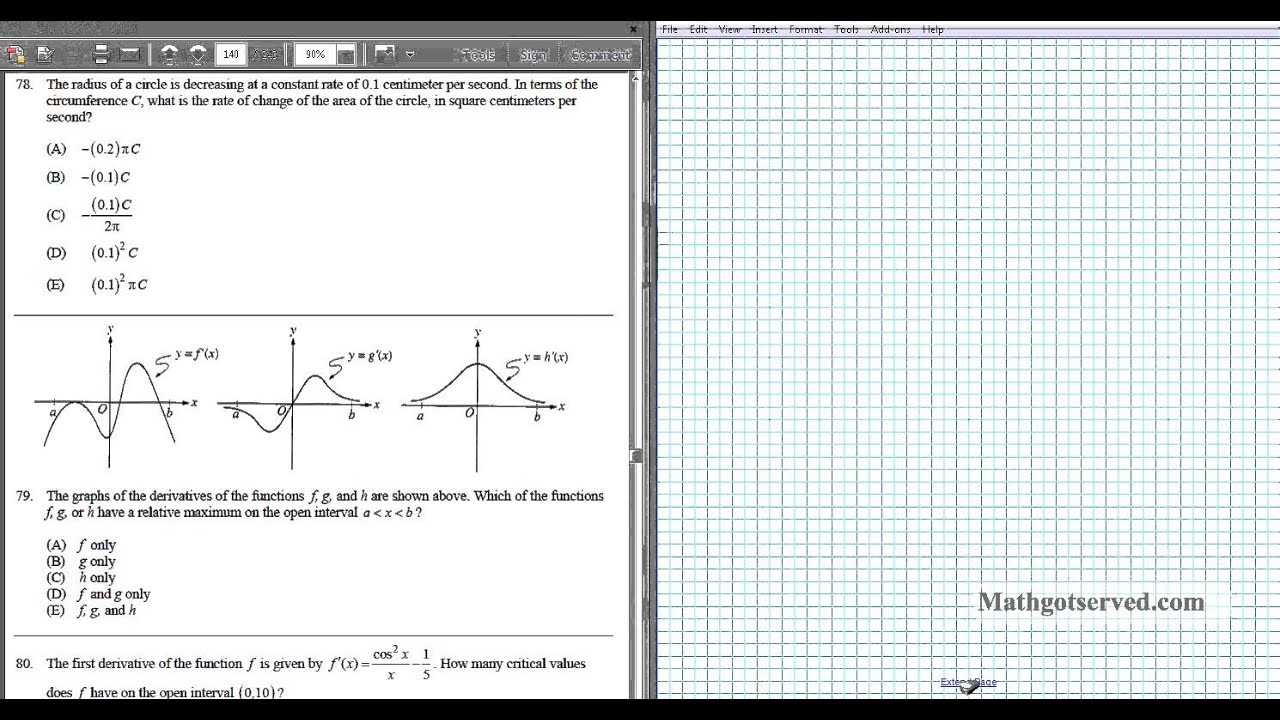



Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
The graph of f(x)=1/x3 is a visual presentation of the function in the plane On the given graph you can find all of the important points for function f(x)=1/x3 (if they exist) You can always share this solution See similar equations Graph of y=(x^2/4)(7x/4)2 Graph of x^210x21=0 Graph of x=3 Graph of 11x8>3x15 Graph of x^2xy=4 Graph of f(x)=(2x1)/(4x^2Short Solution Steps f ( x ) = 3 x ^ { 2 } \frac { 3 } { x ^ { 2 } } f ( x) = 3 x 2 − x 2 3 To add or subtract expressions, expand them to make their denominators the same Multiply 3x^ {2} times \frac {x^ {2}} {x^ {2}} To add or subtract expressions, expand them to make their denominators the same Multiply 3 x 2 times x 2 x 2Sketch the graph of f(x)=x^24x finding the vertex, axis of symmetry and all intercepts
· Refer to the explanation Graph f(x)=(x2)^21 is a quadratic equation in vertex form f(x)=a(xh)^2k, where a=0, h=2, k=1 In order to graph a parabola, the vertex, x and yintercepts, and additional points need to be determined Vertex maximum or minimum point of a parabola The vertex is the point (h,k) (2,1) Yintercept value of y when x=0 Substitute y for f(x2 = e− 2 = f(x) and lim x→±∞ e− (−x)2 2 = 0, the graph is symmetry wrt the yaxis, and the xaxis is a horizontal asymptote • Wehave f0(x) = e−x 2 2 (−x) = −xe− x2 2 • Thus f ↑ on (−∞,0) and ↓ on (0,∞) • Atx = 0, f 0(x) = 0 Thus f(0) = e = 1 is the (only) local and absolute maximum • Fromf0(x) = − · There are two horizontal tangents at 0 and at 2 graph {x^3 3x^2 842, 1378, 662, 448} You can start by setting x = 0 that gives you y = f (0) = 0 so your curve passes through the origin When x → ∞ f (x) → ∞ as well while when x → − ∞ then f (x) → − ∞
Draw the graph of f(x) = (x − 2) 2 − 1 (or f(x) = x 2 − 4x 3) and compare it to the basic graph g(x) = x 2 If we use the same method as in the previous example we can guess that the graph has moved two units to the right and one unit down Now we will check this by making a table of values, beginning with x = 0 and drawing the graphThe equation is in standard form xf=x^ {3}4x^ {2}11x30 x f = x 3 − 4 x 2 − 1 1 x 3 0 Divide both sides by x Divide both sides by x \frac {xf} {x}=\frac {\left (x5\right)\left (x2\right)\left (x3\right)} {x} x x f = x ( x − 5) ( x − 2) ( x 3) Dividing by x undoes the multiplication by x2 x7, x > 3 Chapter 1 12 Graphs of Functions



Draw The Graph Of The Function F X Max X X 2 And Write
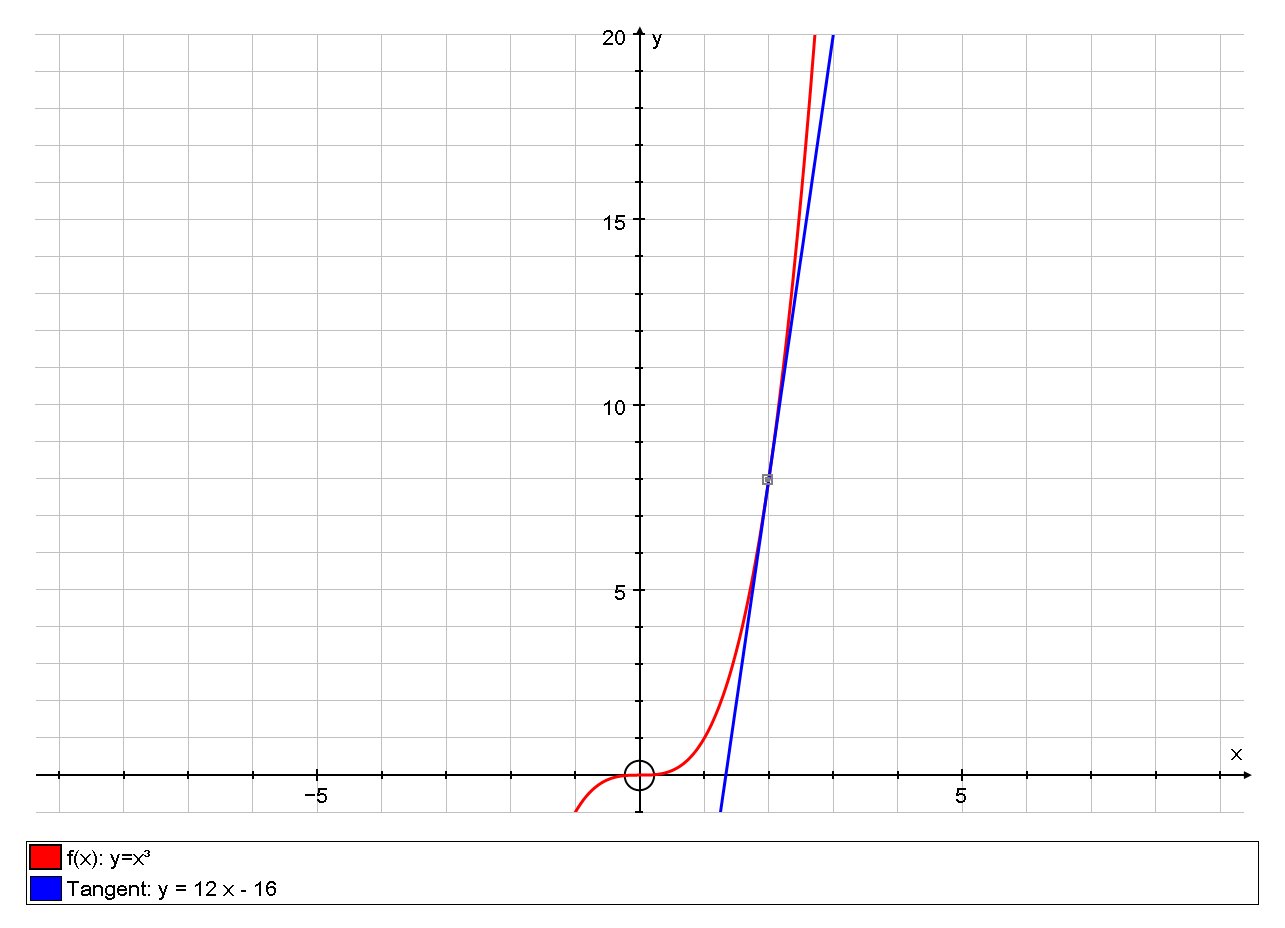



How Do You Find The Equation Of The Tangent Line To The Graph Of F X X 3 At Point 2 8 Socratic
F ( x) = 3 x 3 − x 2 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 2 and q divides the leading coefficient 3 One such root is 1 Factor the polynomial by dividing it by x1 Polynomial 3x^ {2}3x2 is not factored since it does not have any rational rootsGraph f(x)=(x2)(x3)(x1) Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term Tap for more steps Raise to the power of Multiply by Multiply by by adding the exponents Tap for more steps Multiply by Tap for more steps Raise to the power of Use the power rule to combine exponentsUploaded By EarlLarkPerson258 Pages 27 This preview shows page 14 26 out of 27 pages Example 7 Sketch the graph of f (x) = 4, x ≤ 5;x1,5 < x ≤ 3;




How To Graph The Domain Of Question 11 Calculus
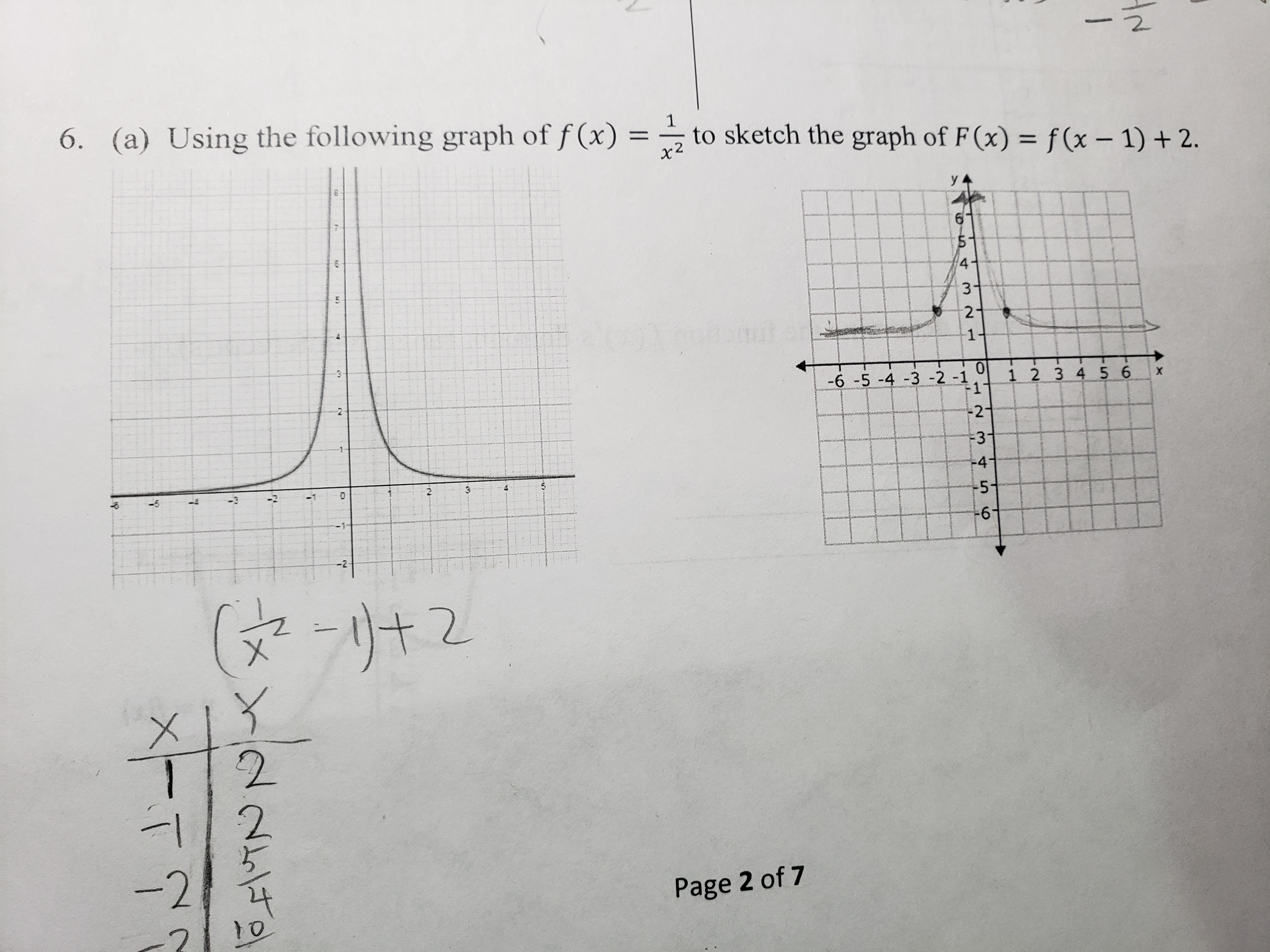



Answered 2 0 1 2 3 4 5 6 A Using The Bartleby
Functions & Graphing Calculator \square!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and capabilities to the broadest possibleUse a graph of f(x) to determine the value of f(n), where n is a specific xvalueTable of Contents0000 Finding the value of f(2) from a graph of f(x)002
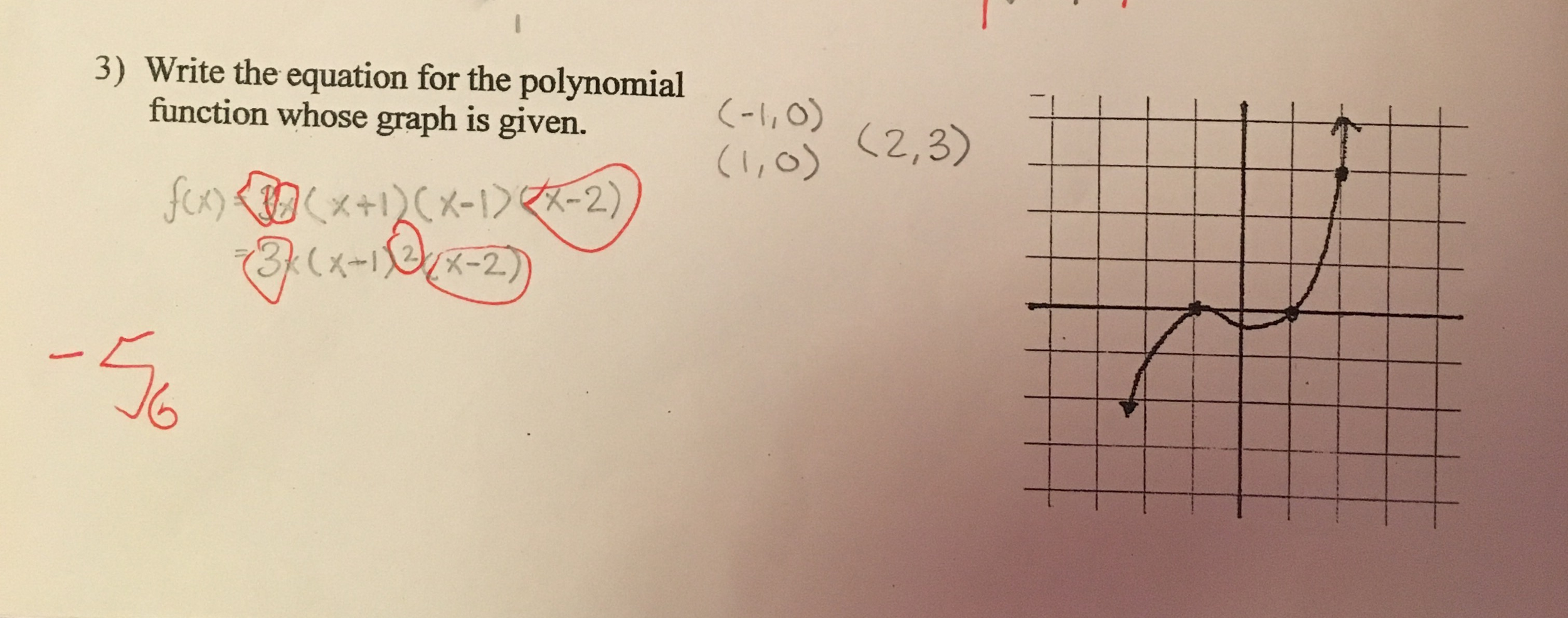



Solved Sketch A Graph Of F X 2x X 2 2 X 3 Writ Chegg Com




5 2 Properties Of Quadratic Functions In Standard Form Pages 1 5 Flip Pdf Download Fliphtml5
· The graph will be the same width as the parent graph f(x) = x², but the vertex has been shifted to (1, 2) Explanation Since the value of a, the coefficient of x², is 1, this means the graph has not been stretched or shrunk However, since the function is different than f(x)=x², we know that the vertex is not at (0, 0) We can write the function in vertex form to find the newHere is a picture of the graph of g(x) = 3(x)1/2 Since c = 3 > 1, the graph is obtained from that of f(x) = x1/2 by stretching it in the ydirection by a factor of c = 3 Reflection about the x axis The graph of y = f (x) is the graph of y = f (x) reflected about the x axis Here is a picture of the graph of g(x) = (x 2 1) It is obtainedGraph f(x)=(x2)^23 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focus Tap for more steps Find the distance from the vertex to a focus of the parabola by using the following formula




Answered 14 F X 2 X 3 2 3d 3 Tf X Bartleby




The Graph Of F X X 2 Is Shown Use The Parabola Tool To Graph G X 9 X 1 X 2 2graph The Brainly Com
I assume you know how to graph For each value of x the point on f (x) = x^2 4 is 4 units below the point with the same x value on g (x) = x^2 so take the graph of g (x) and move it down 4 units to obtain the graph of f (x) I'm confused by second part of your question I only see 3You can clickanddrag to move the graph around If you just clickandrelease (without moving), then the spot you clicked on will be the new center To reset the zoom to the original click on the Reset button Using "a" Values There is a slider with "a =" on it You can use "a" in your formula and then use the slider to change the value of "aThe graph of f(x)=3x−x2 a The domain is all real x The range is all real y where y ≤ 225 b f(q)=3q −q2 c f(x2)=3(x2)−(x2)2 =3x2 −x4 Example The graph of the function f(x)=(x−1)2 1 is sketched below The graph of f(x)=(x−1)2 1 –1 x 2 4 y 021 Mathematics Learning Centre, University of Sydney 5 State its domain and range Solution The function is defined for all real x




Graphs Of Rational Functions Vertical Asymptotes Video Khan Academy
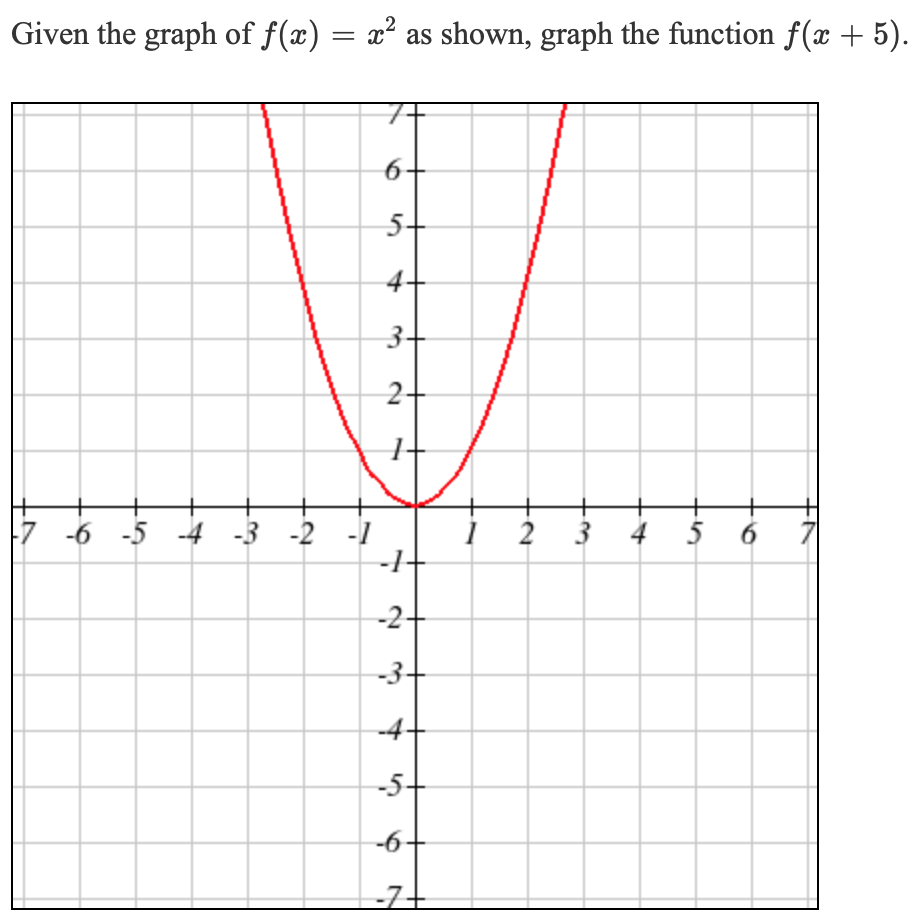



Solved Given The Graph Of F X X2 As Shown Graph The F Chegg Com
· As an example, if I have f(x)=(x3) 3, then the graph would translate three units to the left Vertical Movement Trying to find out whether the graph would move upwards or downwards means considering the form y=f(x) ±c If c is positive, the graph moves upward If c is negative, the graph moves downward For instance, if I have f(x)=(x) 3 3, then the graph would translate · Set #y=0=2/3(x2)^5# #(x2)^2=3/2(1/2) = 3/4# #sqrt((x2)^2)=sqrt(3/4)# #x=2sqrt(3/4)# You can go further with this using complex numbers However, you do not need to as you are only plotting/sketching the graphDraw the graph of the following function {eq}f(x)=x^23 {/eq} Transformations of Graphs We know the graphs of a few basic functions, such as the square root function




Finding The Intersection Of Two Functions Graphs Mathematics Stack Exchange
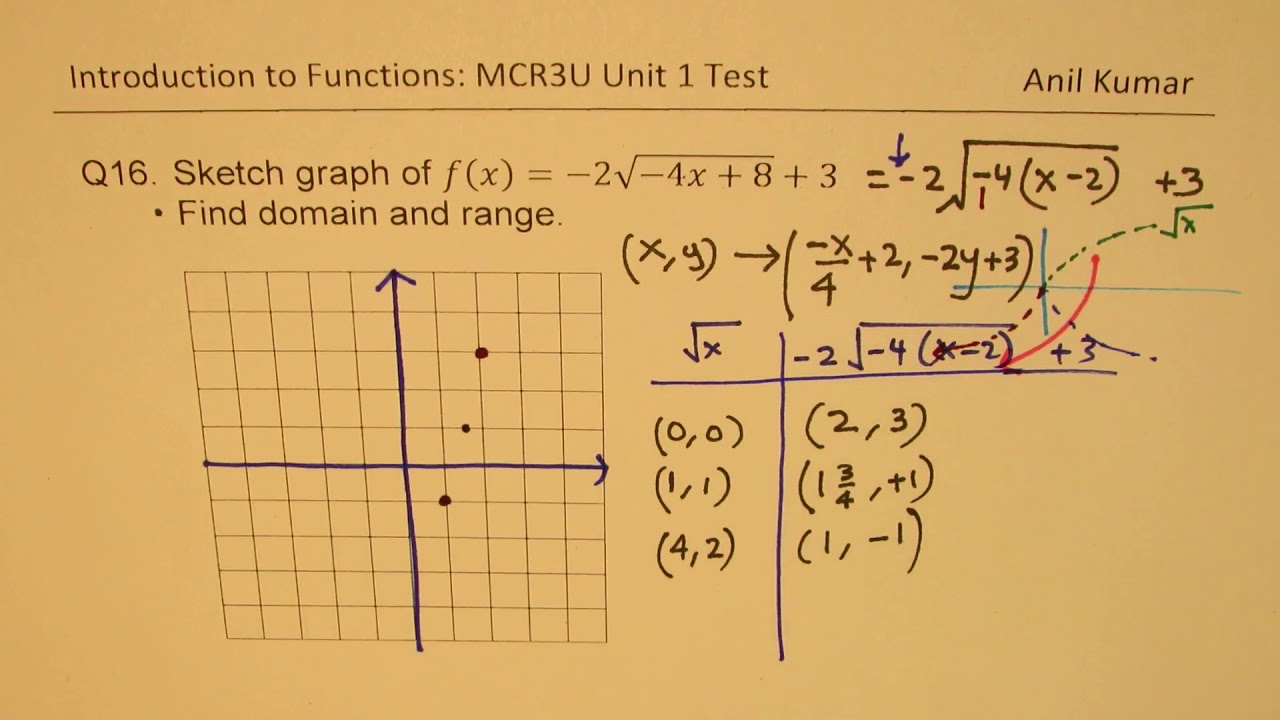



How To Sketch Graph Of F X 2 4x 8 3 Transformed Square Root Function Youtube
Graph f(x)=(x3)^32 Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term Tap for more steps Subtract from Raise to the power of Multiply by Add and The final answer is Convert to decimal Find the point at Tap for more steps Replace the variable with in the expression3,3 ii 1 2 y = f(x) y = 2f(x), which is a stretch with scale factor 2 in the ydirection P is transformed to (4, 6) iii y = f(x − 5) is a translation by 5 0 , or five units right to the P is transformed to (9, 3) iv −y = f(x) y = −f(x), which is a reflection of the curve in the xaxis (4, −3) v 2(y 2) = f(x) yCourse Title MASS 0;




How To Graph A Parabola F X 2 3x 2 5 Socratic
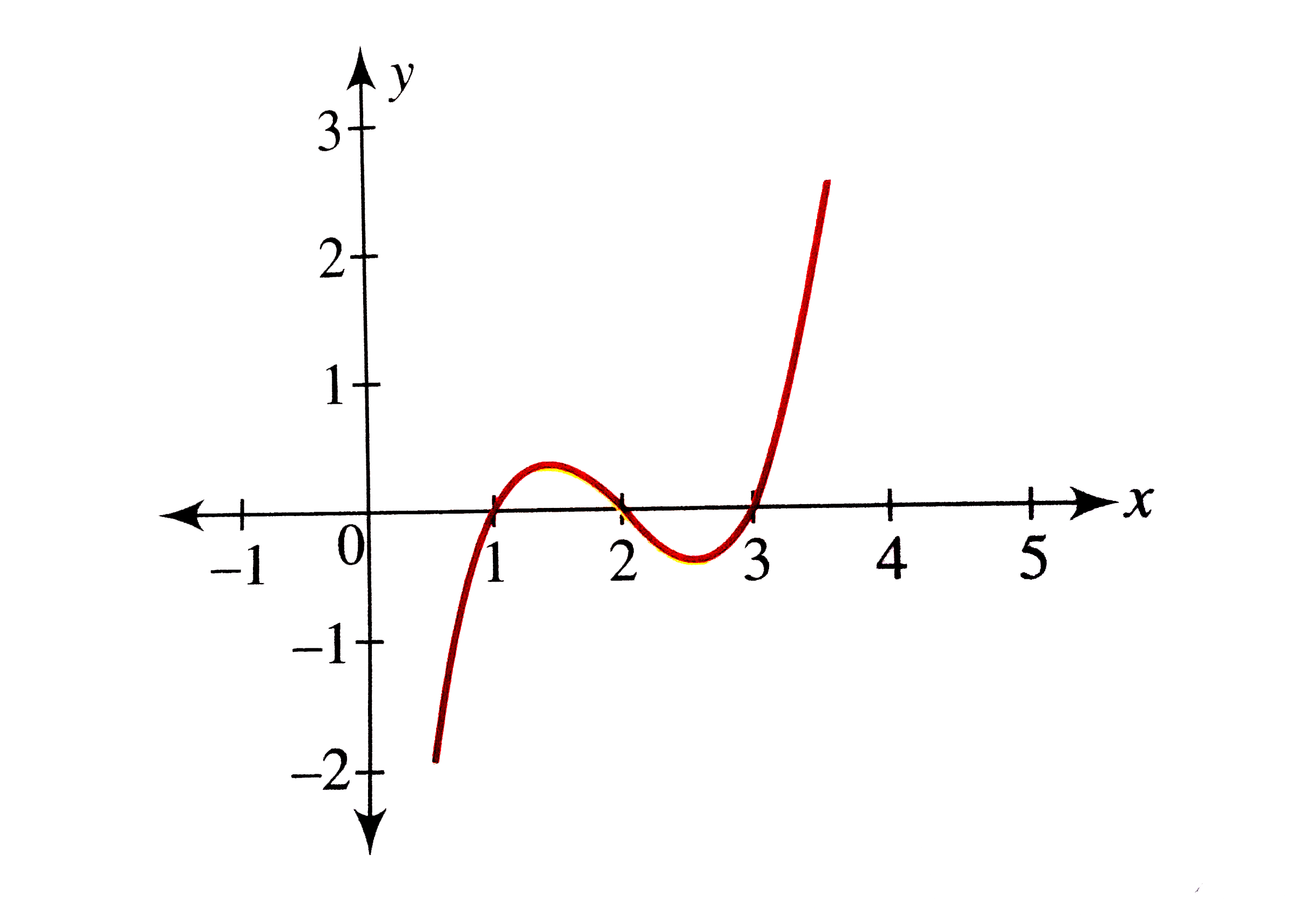



Draw The Graph Of F X X 1 X 2 X 3
Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and images · The graph of a function f(x,y) is the set of all points (x,y,z) in space such that (x,y) is in the domain of f and z=f(x,y) Here are a few examples Example 1 f(x,y) = x 2 y 2 Example 2 f(x,y) = x 2y 2 Example 2 f(x,y) = ex 2y 2 Example 3 In an example on Monday, we looked at the cost function C(x,y) = 10/x10/y3xy Its graph is shown below From the side view, itSOLUTION 7 The domain of f is all xvaluesNow determine a sign chart for the first derivative, f' Then f'(x) = 1 3 (1/3) x 1/31 = 1 x2/3 = 0 when x 2/3 1 = 0 Thus, x 2/3 = 1 so that and x = 1 or x = 1 In addition, note that f' is NOT DEFINED at x=0 To avoid using a calculator, it is convenient to use numbers like x= 8, 1/8, 1/8, and 8 as "test points" to construct the
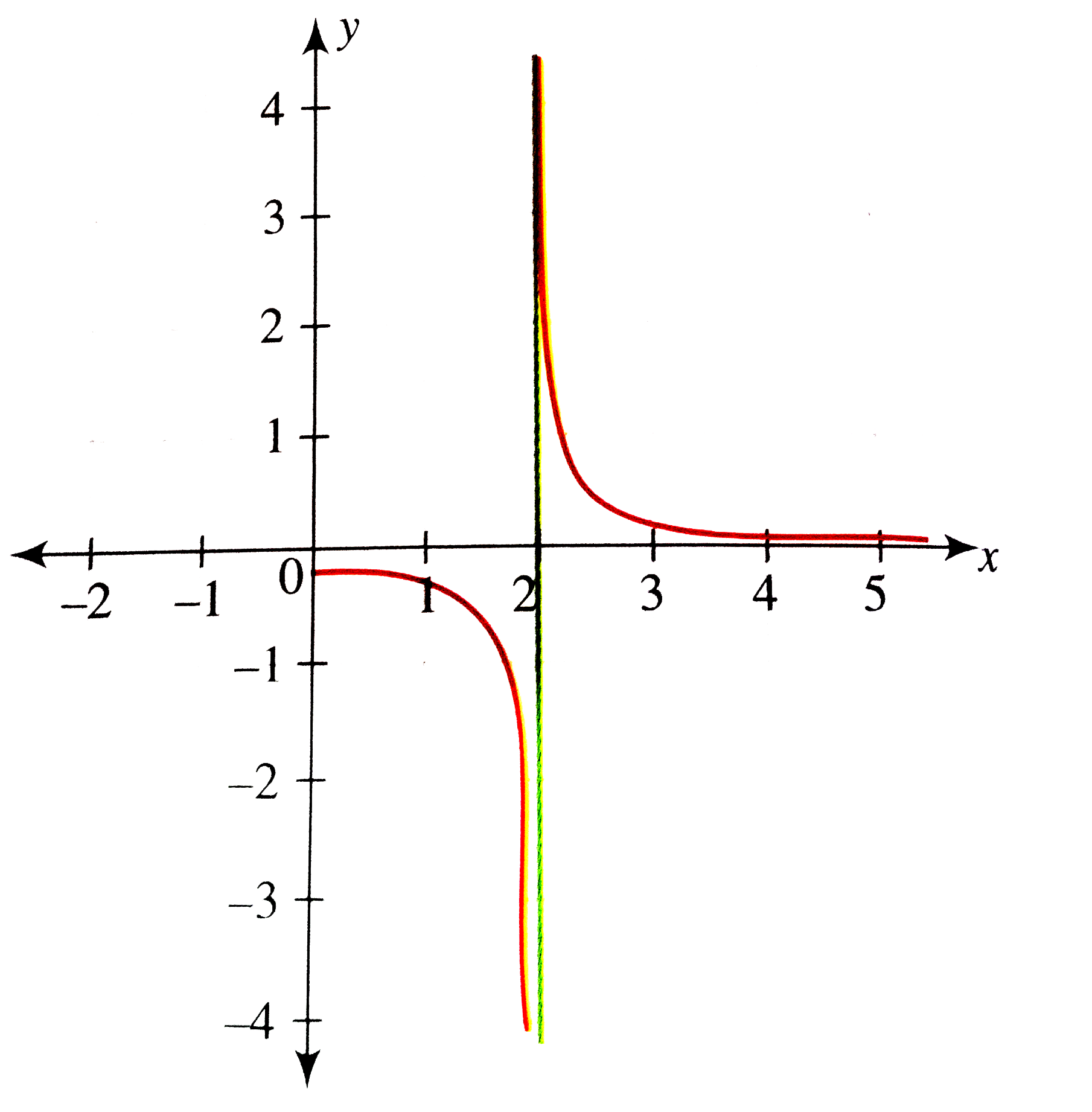



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4




Graphing Square And Cube Root Functions Video Khan Academy
Example 7 Sketch the graph of f x 4 x 5 x 1 5 x 3 2 x 7 x 3 Chapter 1 12 Graphs Example 7 sketch the graph of f x 4 x 5 x 1 5 x 3 2 x School St John's University;The Function which squares a number and adds on a 3, can be written as f(x) = x 2 5 The same notion may also be used to show how a function affects particular values Example f(4) = 4 2 5 =21, f(10) = (10) 2 5 = 105 or alternatively f x → x 2 5 The phrase "y is a function of x" means that the value of y depends upon the value of x, so y can be written in terms of x (eg yF (x)=x^23x 2 \square!
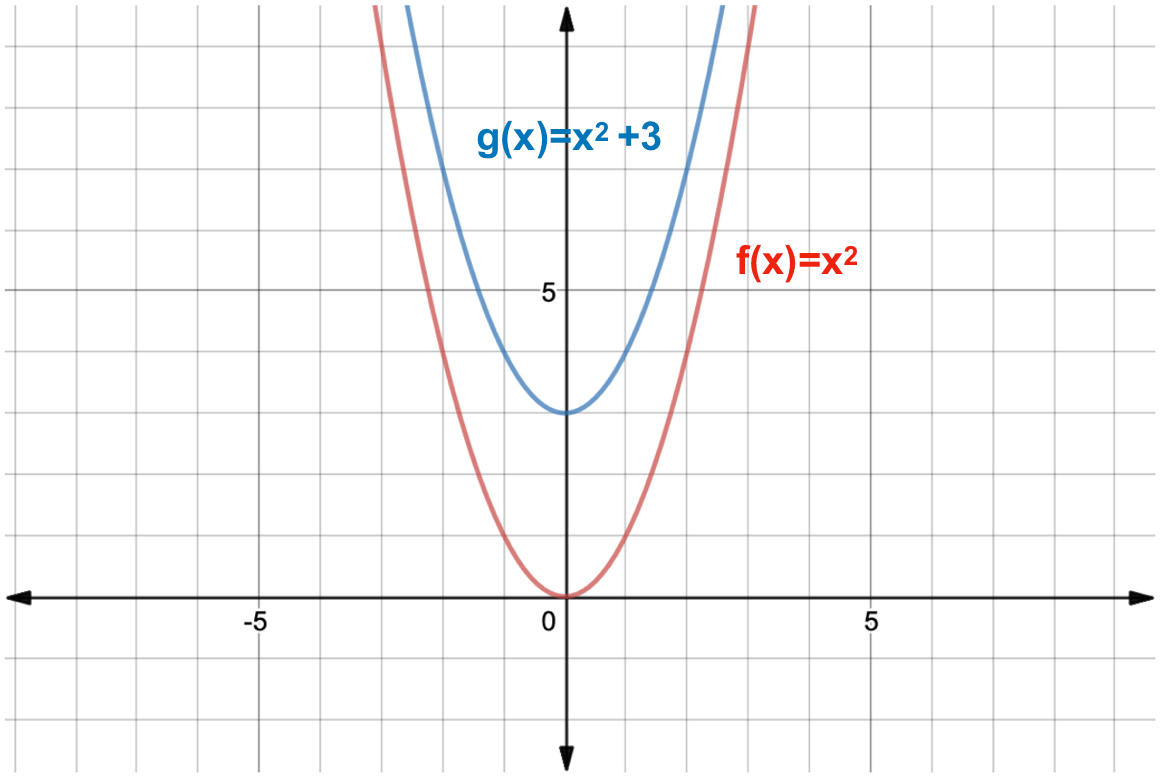



What Is A Function Transformation Expii




Using Transformations To Graph Functions
Plot of the graph of f(x, y) = −(cos(x 2) cos(y 2)) 2, also showing its gradient projected on the bottom plane The graph of the trigonometric function (,) = is {(,, ())} If this set is plotted on a three dimensional Cartesian coordinate system, the result is a surface (see figure) Oftentimes it is helpful to show with the graph, the gradient of the function and severalGraph a quadratic function using transformations · You can scroll in and out and drag the graph window around using a mouse The difference is that the function in this question has squared all of the 3rd roots, so all of the y values are positive (and have the value of the square) x2 3 = (x1 3) = (3√x)2 Here is the graph




Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
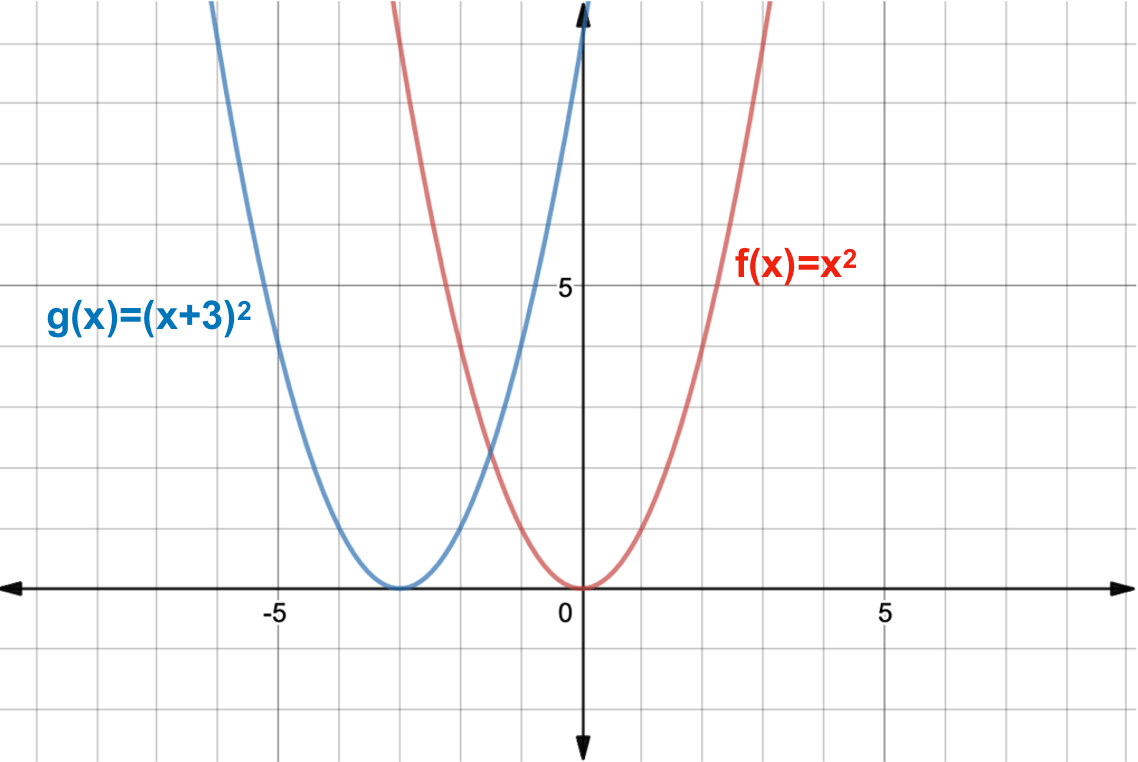



What Is A Function Transformation Expii
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Graph f(x)=x32 Find the absolute value vertex In this case, the vertex for is Tap for more steps To find the coordinate of the vertex, set the inside of the absolute value equal to In this case, Add to both sides of the equation Replace the variable with in the expression Simplify Tap for more steps Simplify each term Tap for more steps Subtract from The absoluteFor instance, the graph for y = x 2 3 looks like this This is three units higher than the basic quadratic, f (x) = x 2 That is, x 2 3 is f (x) 3 We added a "3" outside the basic squaring function f (x) = x 2 and thereby went from the basic quadratic x 2 to the transformed function x 2 3 This is always true To move a function up, you add outside the function f (x) b is f (x




Which Graph Represents F X X 2 2 3 Brainly Com
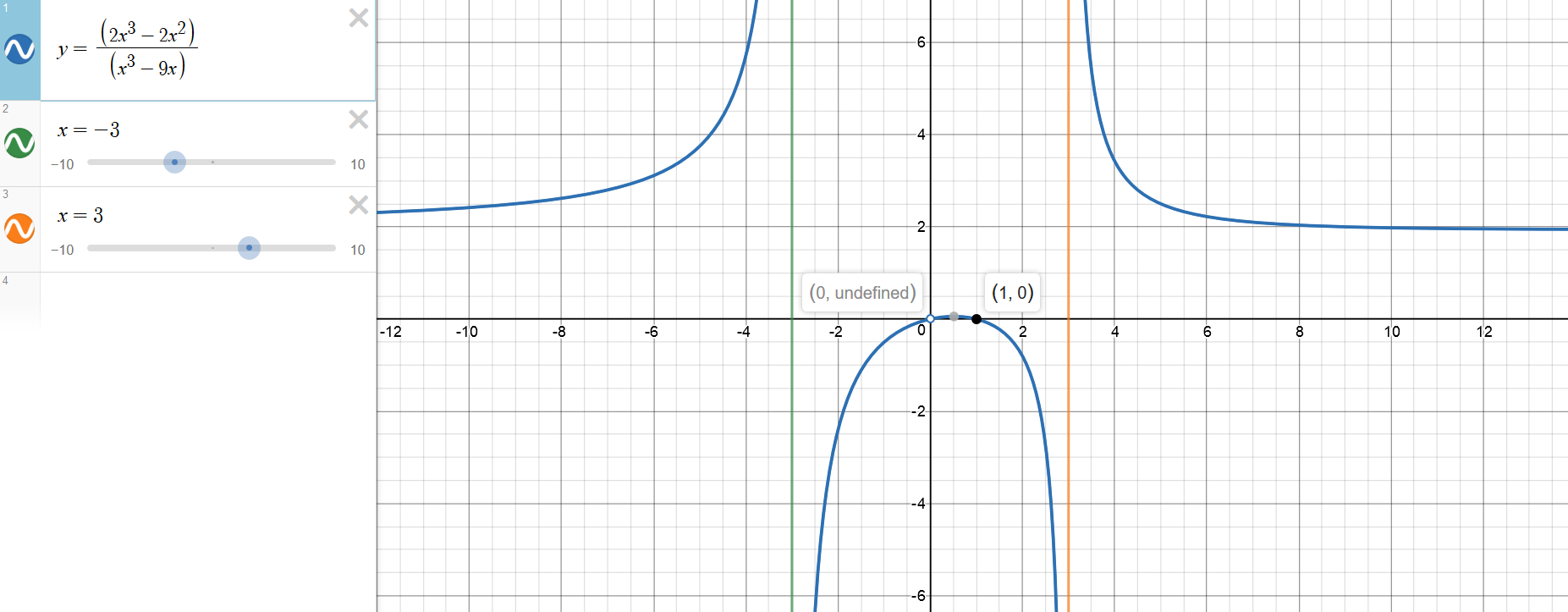



How Do You Graph F X 2x 3 2x 2 X 3 9x Using Holes Vertical And Horizontal Asymptotes X And Y Intercepts Socratic
In this math video lesson I review how to graph the exponential equation y=2^x by making a table The table helps when graphing these types of equations #eGRAPH OF f(x) = x^3 f(x) = x^3 graph how to draw graph of f(x)=x^3 y = x^3 graphNCERT CLASS 11 MATHS SOLUTIONS ex 23SUBSCRIBE TO MY CHANNEL TO GET MORE UPDAGraph f (x)=2 (3)^x f (x) = −2(3)x f (x) = 2 (3) x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0
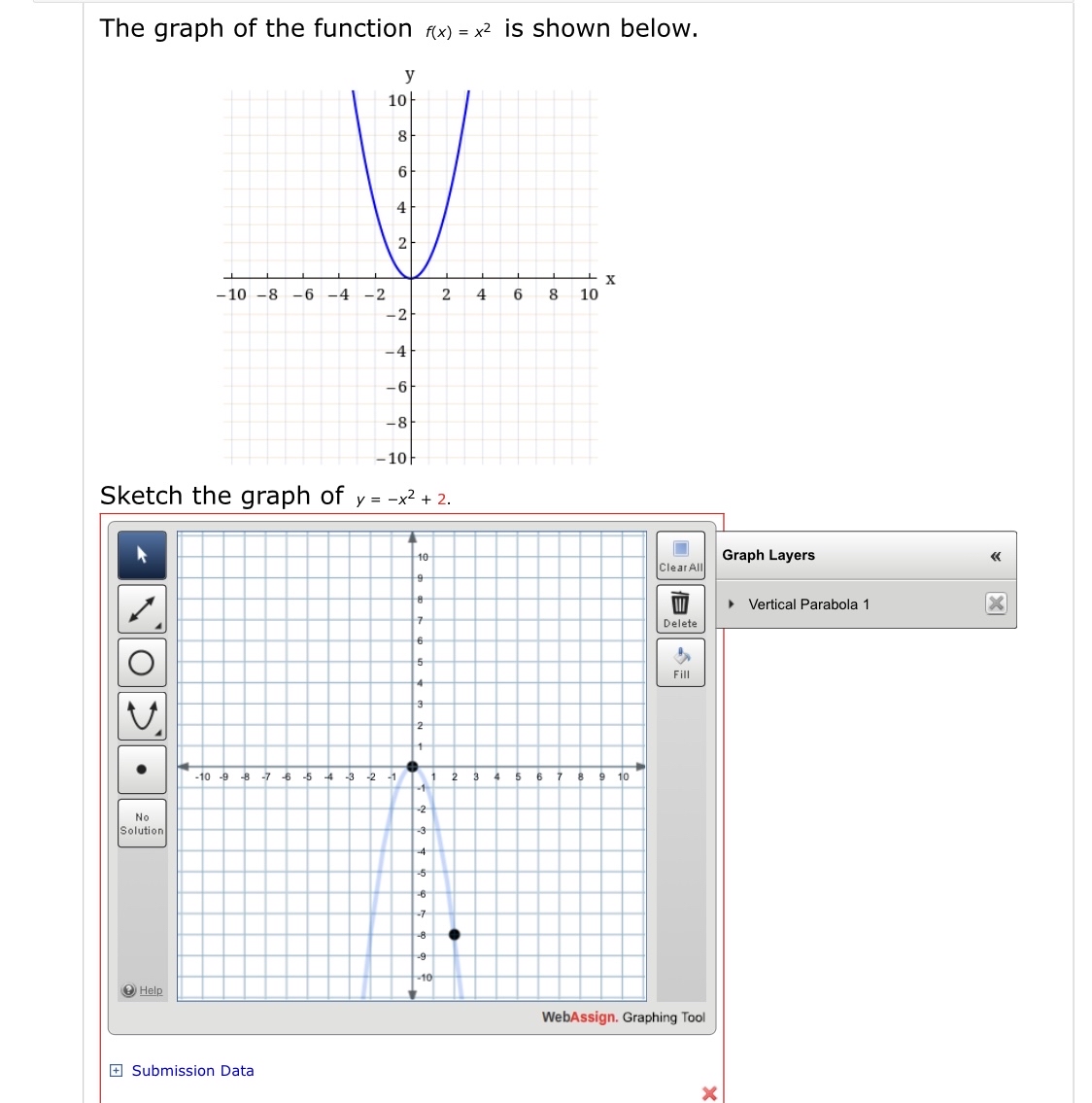



Answered The Graph Of The Function F X X2 Is Bartleby
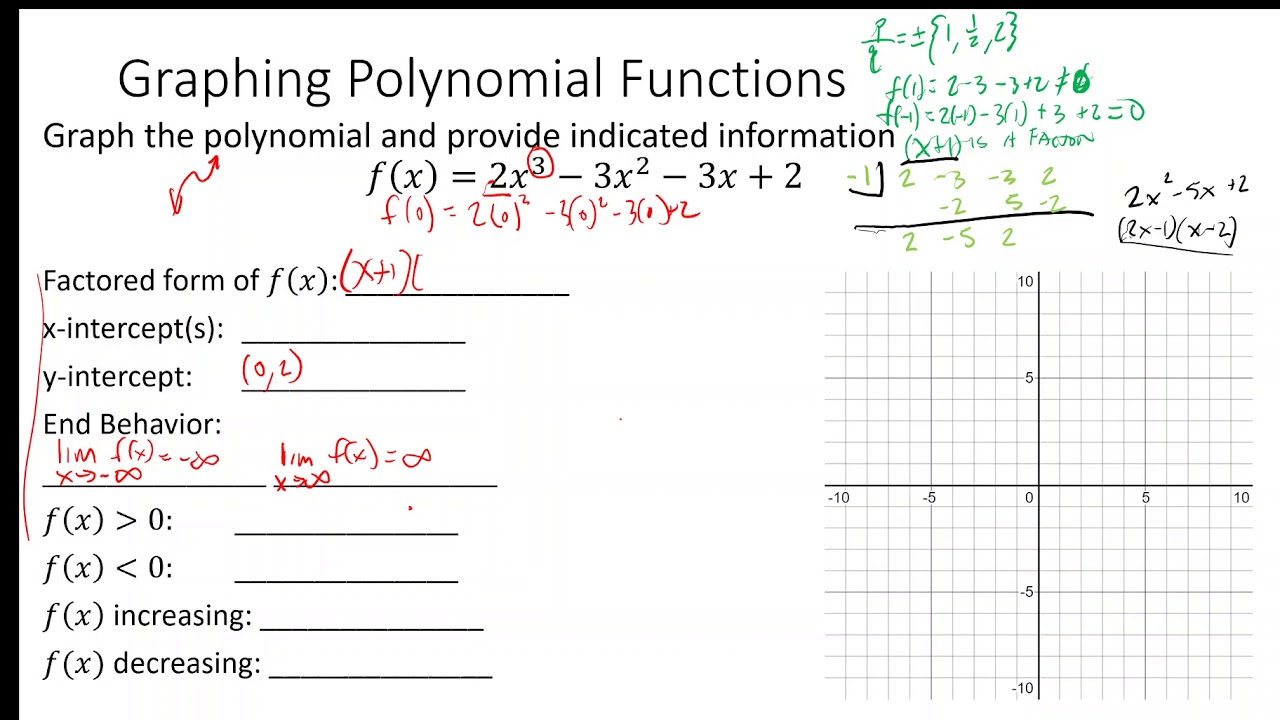



19 Uhs Gribmath Week 2 Graphing Polynomial Functions
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Writing Exponential Functions From Graphs Algebra Video Khan Academy




Finding Values Of Derivative Given F Graph Mathematics Stack Exchange
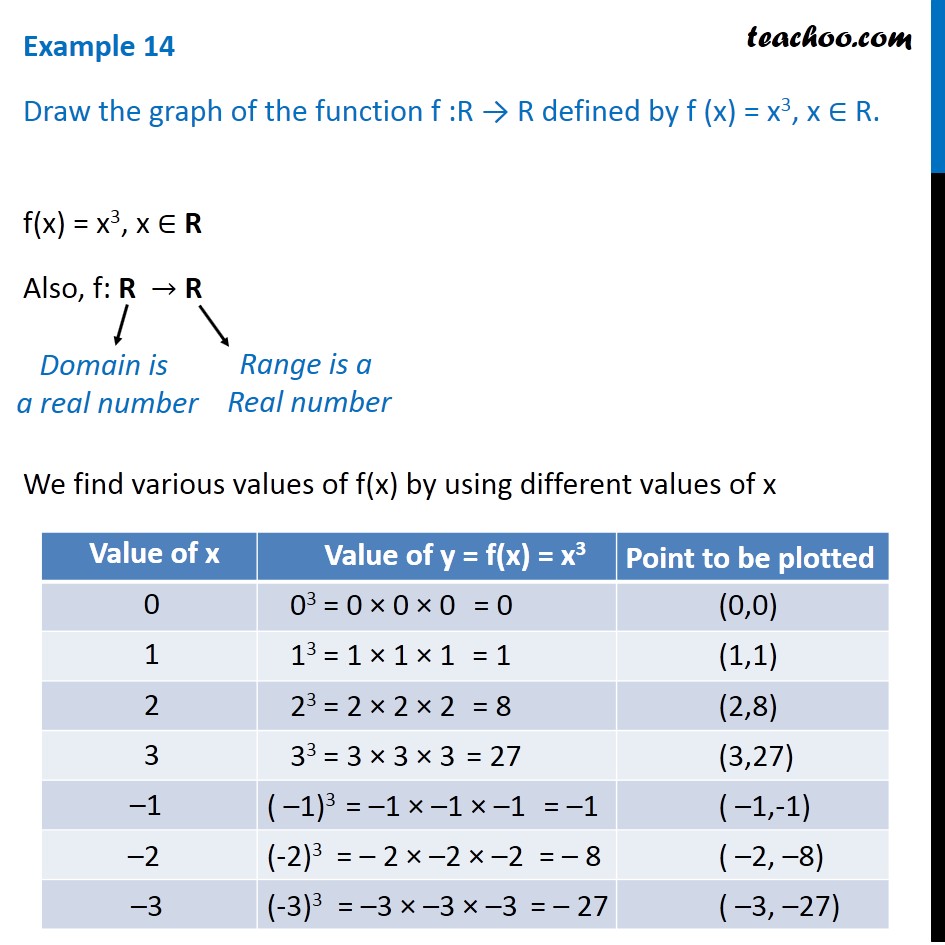



Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11




Please Help Will Give Brainly For Correct Answer Consider The Function F X X 3 2x 2 3 Brainly Com




Bell Assignment 1 Graph The Equation Y X 3 3x 2 1 On Your Gut Then Use The Graph To Describe The Increasing Or Decreasing Behavior Of The Function Ppt Download




Example 13 Define Function Y F X X 2 Complete The Table




Solved The Graph Of F X 3 X 2 2 6 Is A Parabo
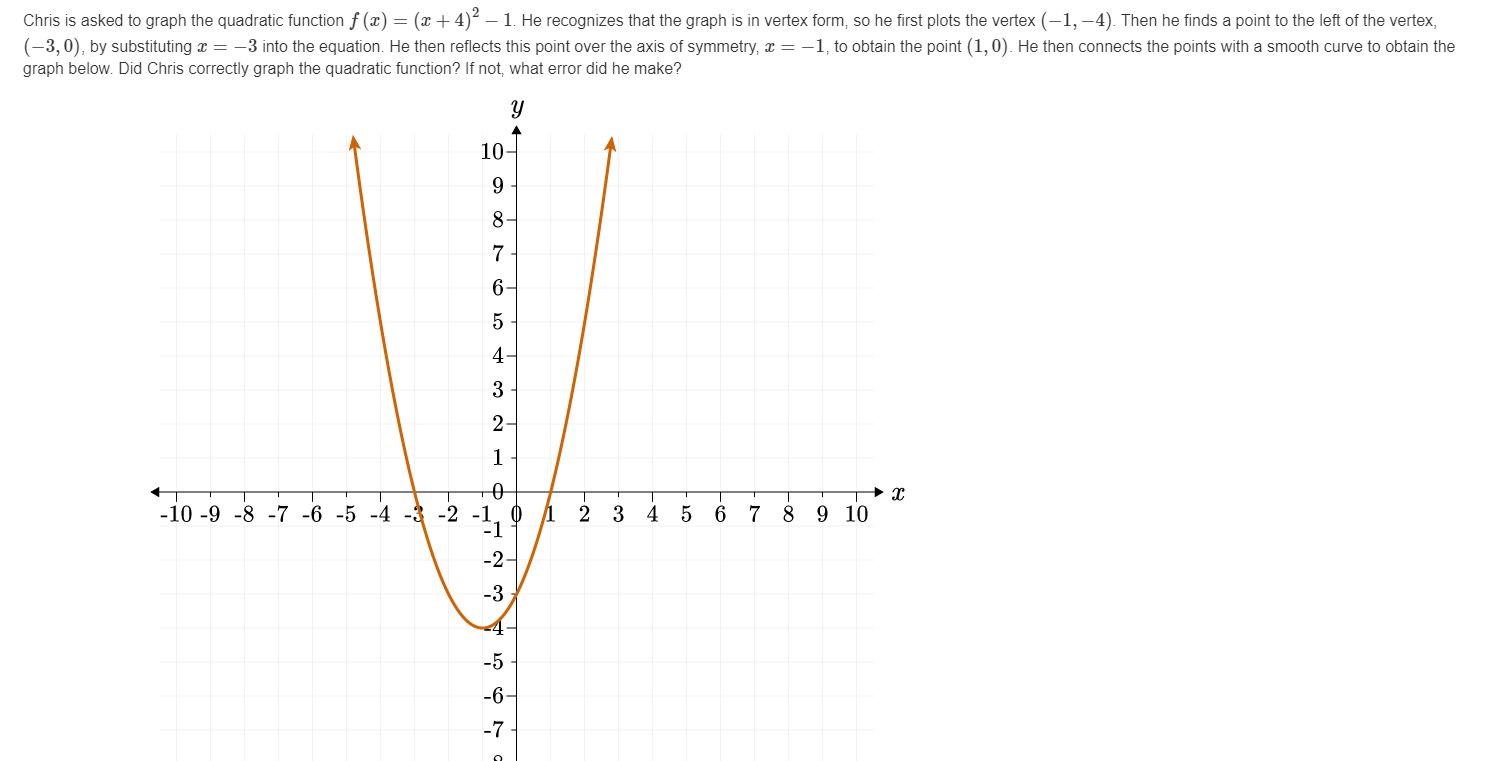



Chris Is Asked To Graph The Quadratic Function F X Chegg Com




Transformations With Functions And Relations
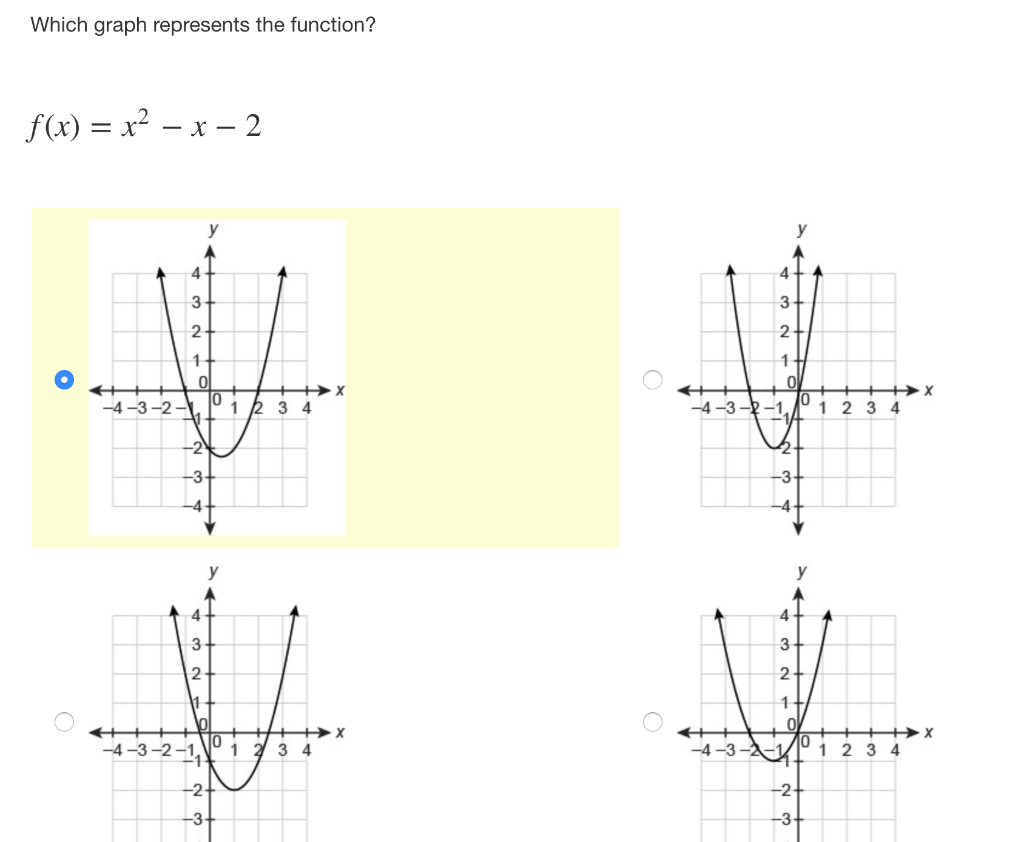



Which Graph Represents The Function X 2 Pifx Chegg Com
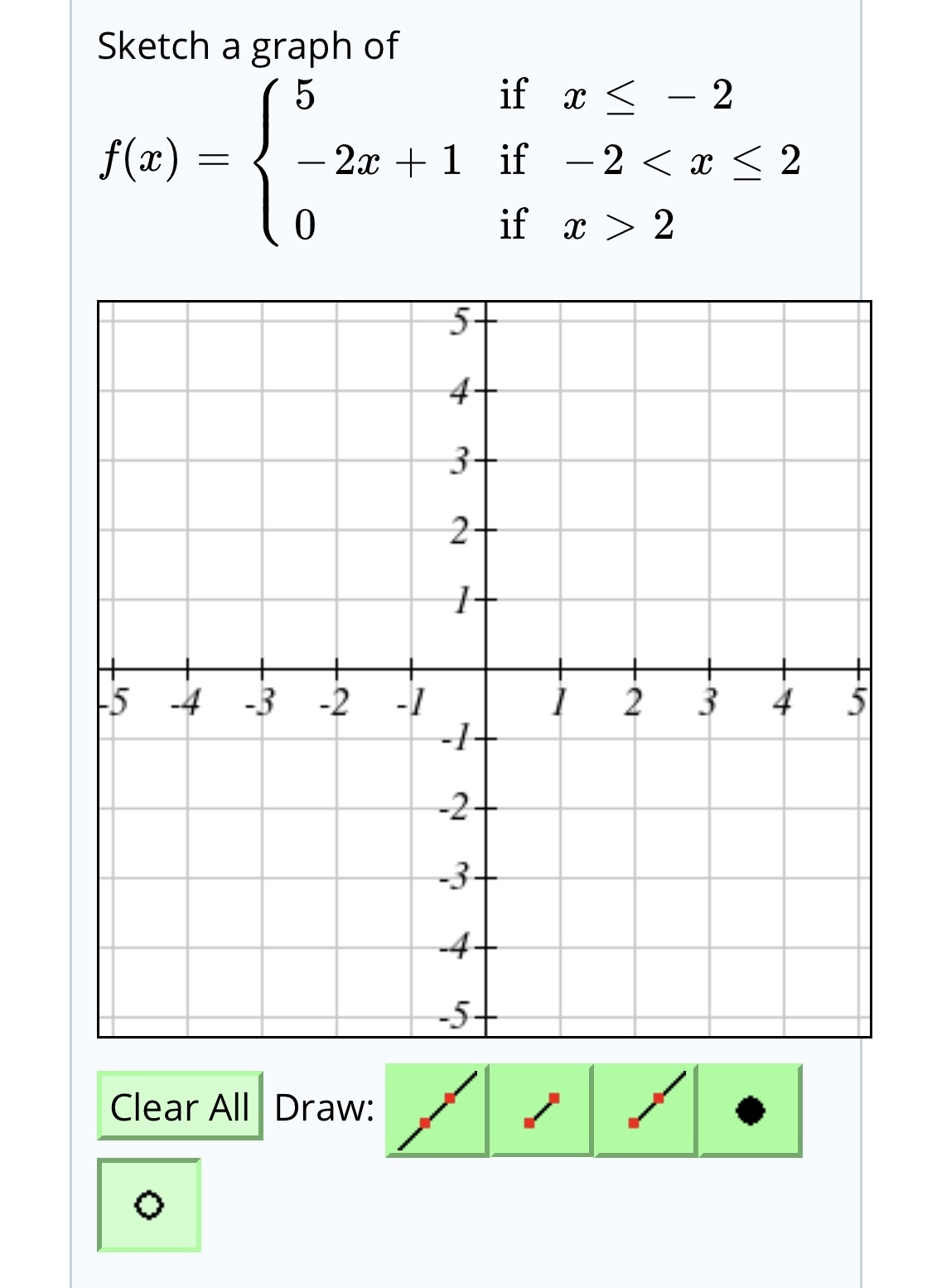



Answered Sketch A Graph Of If X 2 F X 2x Bartleby
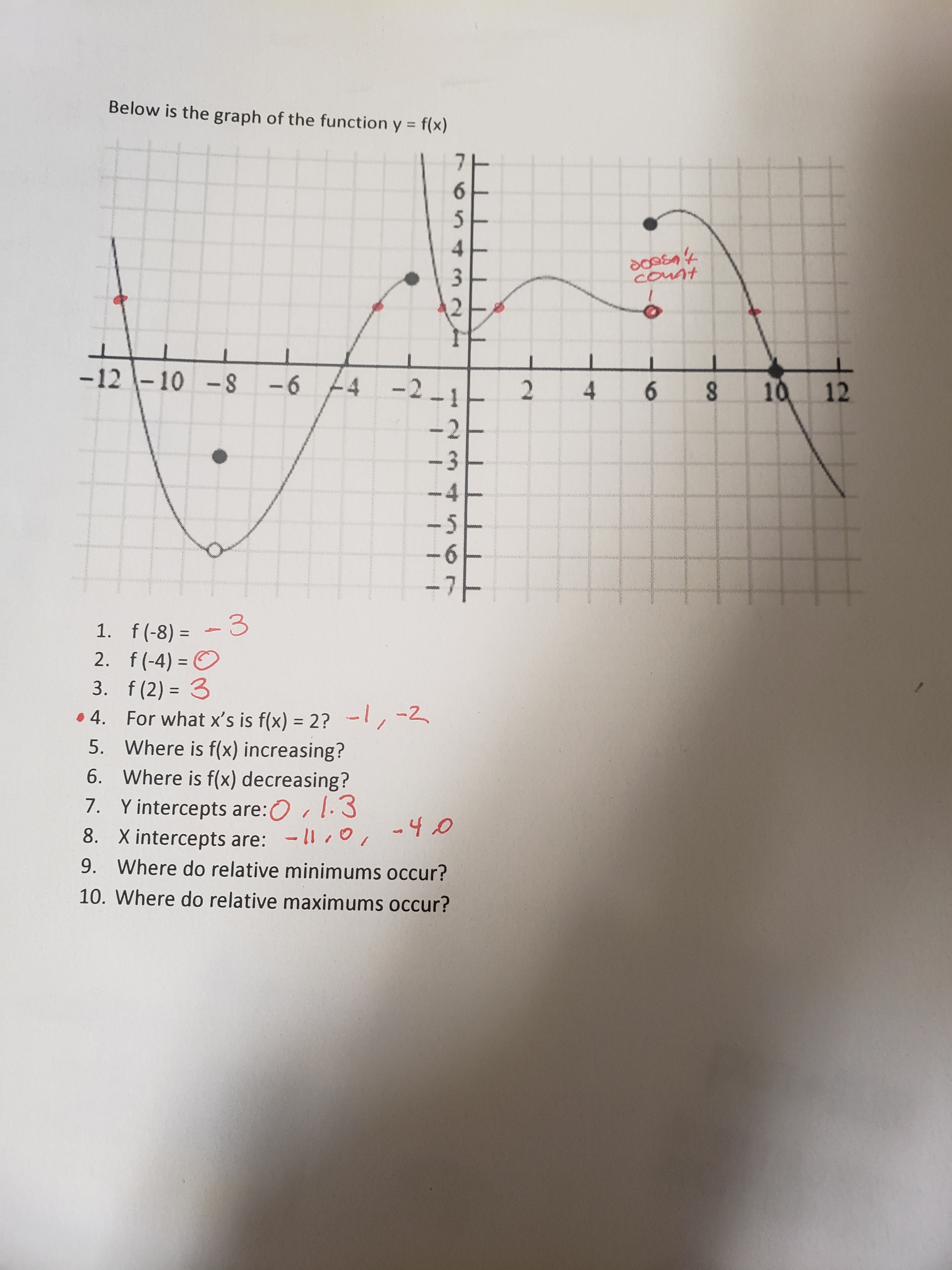



Answered Below Is The Graph Of The Function Y Bartleby
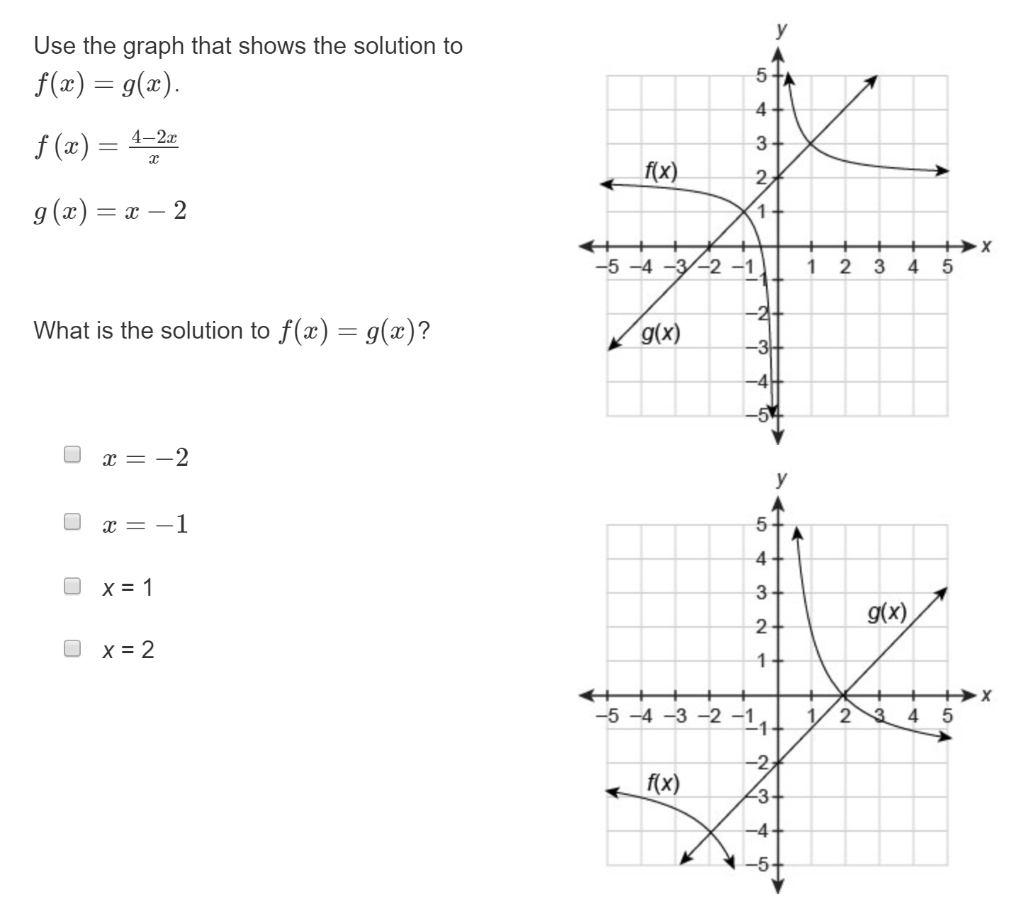



Use The Graph That Shows The Solution To F X G X Chegg Com
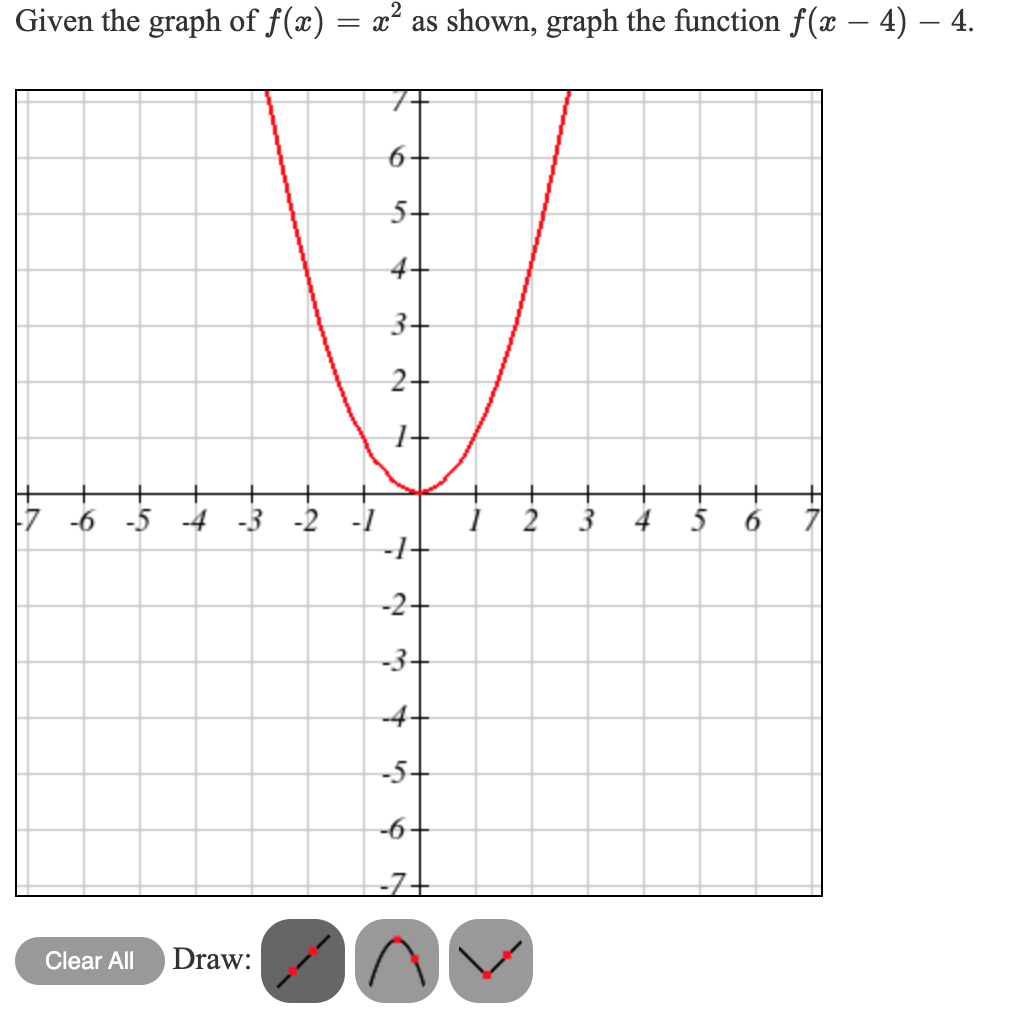



Solved Given The Graph Of F X X2 As Shown Graph The F Chegg Com
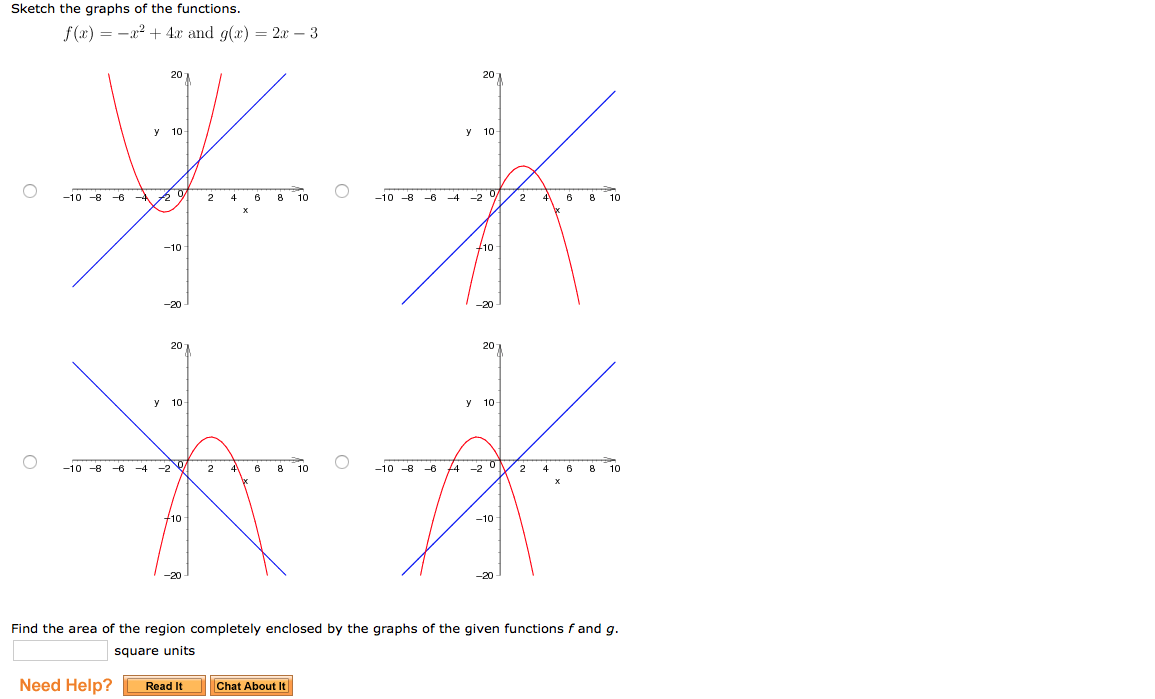



Sketch The Graphs Of The Functions F X X 2 4x Chegg Com
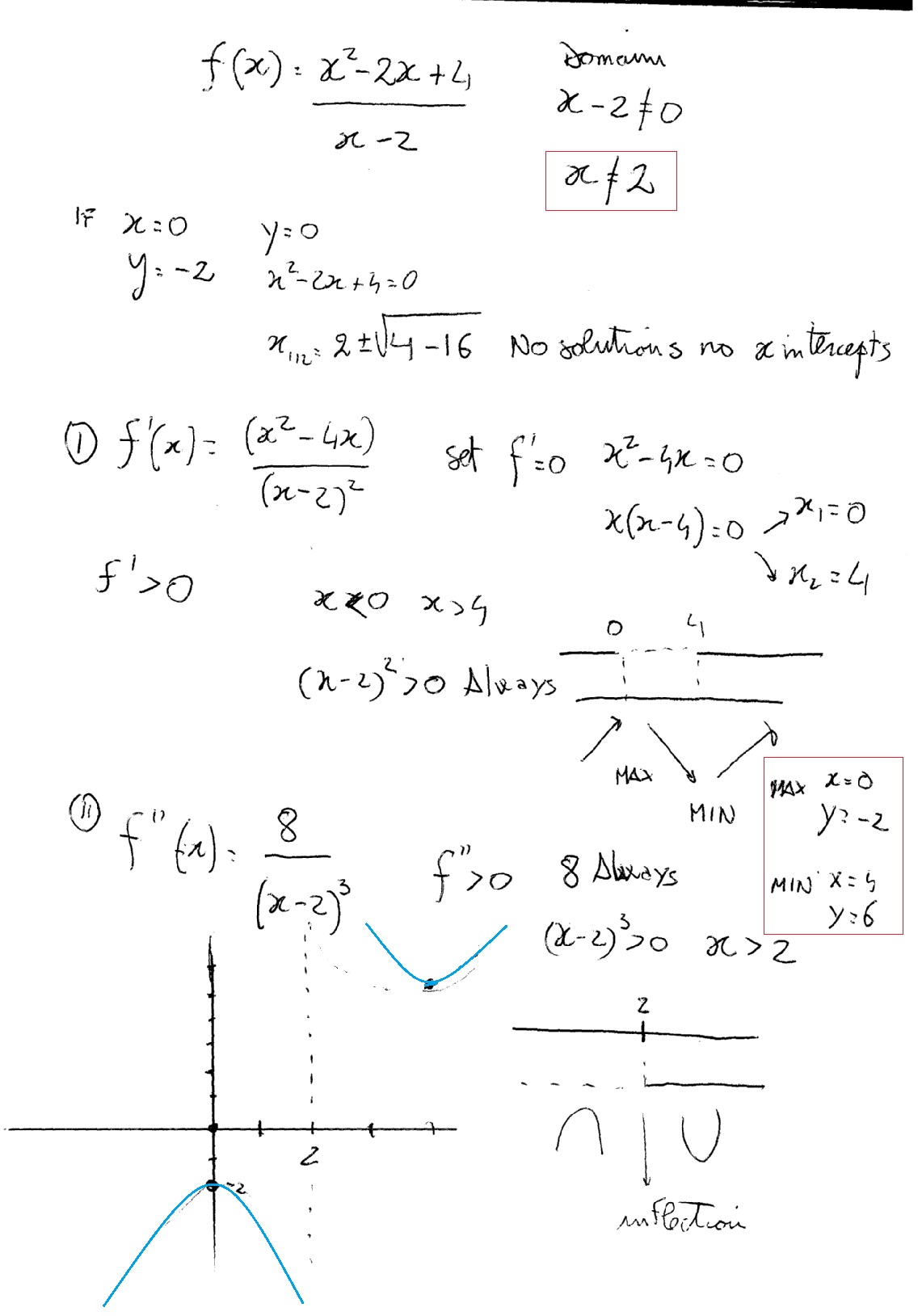



F X X 2 2x 4 X 2 F X X 2 4x X 2 2 F X 8 X 2 3 How To Find The Domain Of F X X And Y Intercepts Vertical Asymptotes The Critical Numbers Concave Up And Down And Sketch Graph Socratic
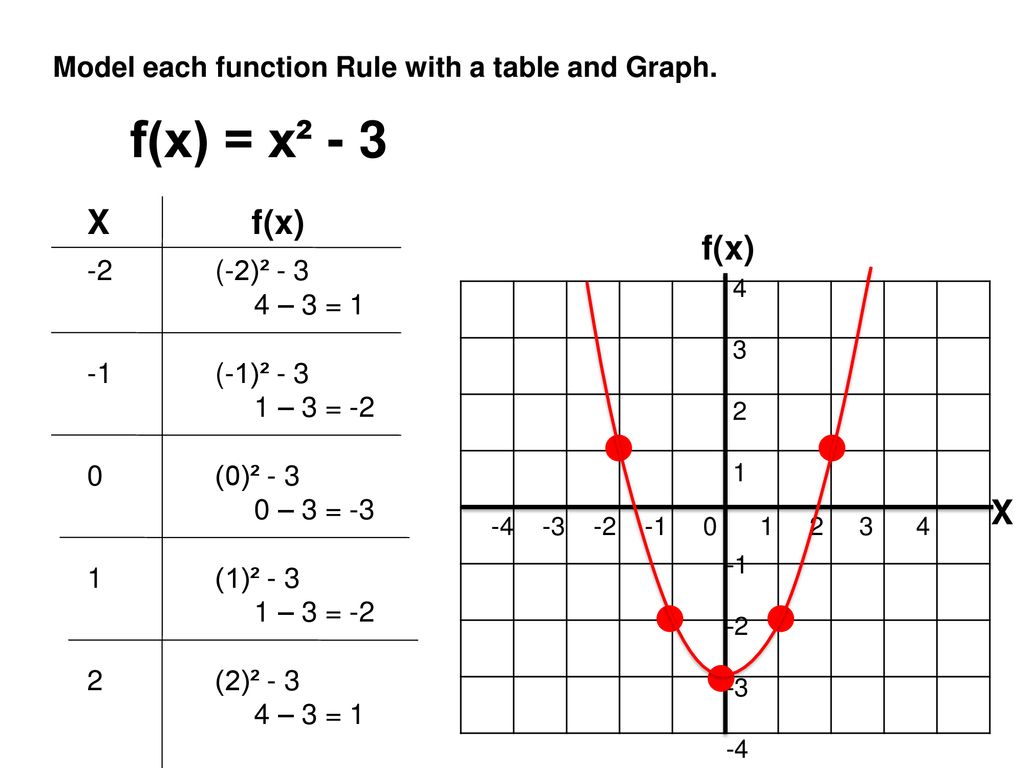



4 16 3 5 2 13 3 4 1 12 3 2 9 2 7 Ppt Download
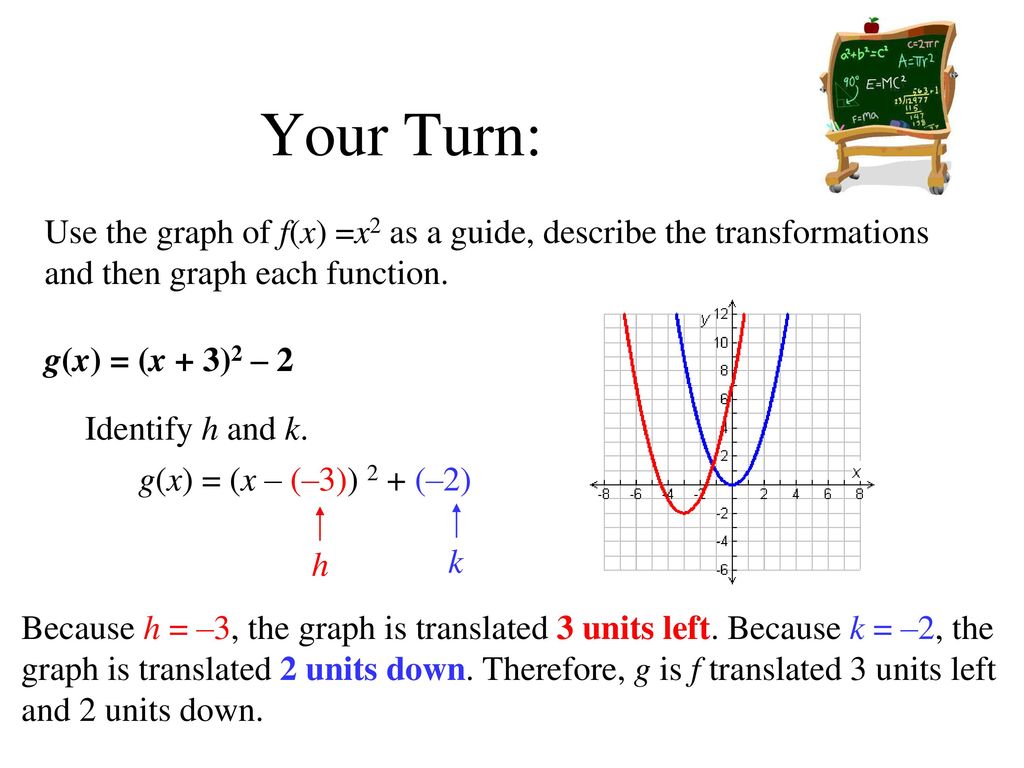



Quadratic Functions And Transformations Lesson Ppt Download
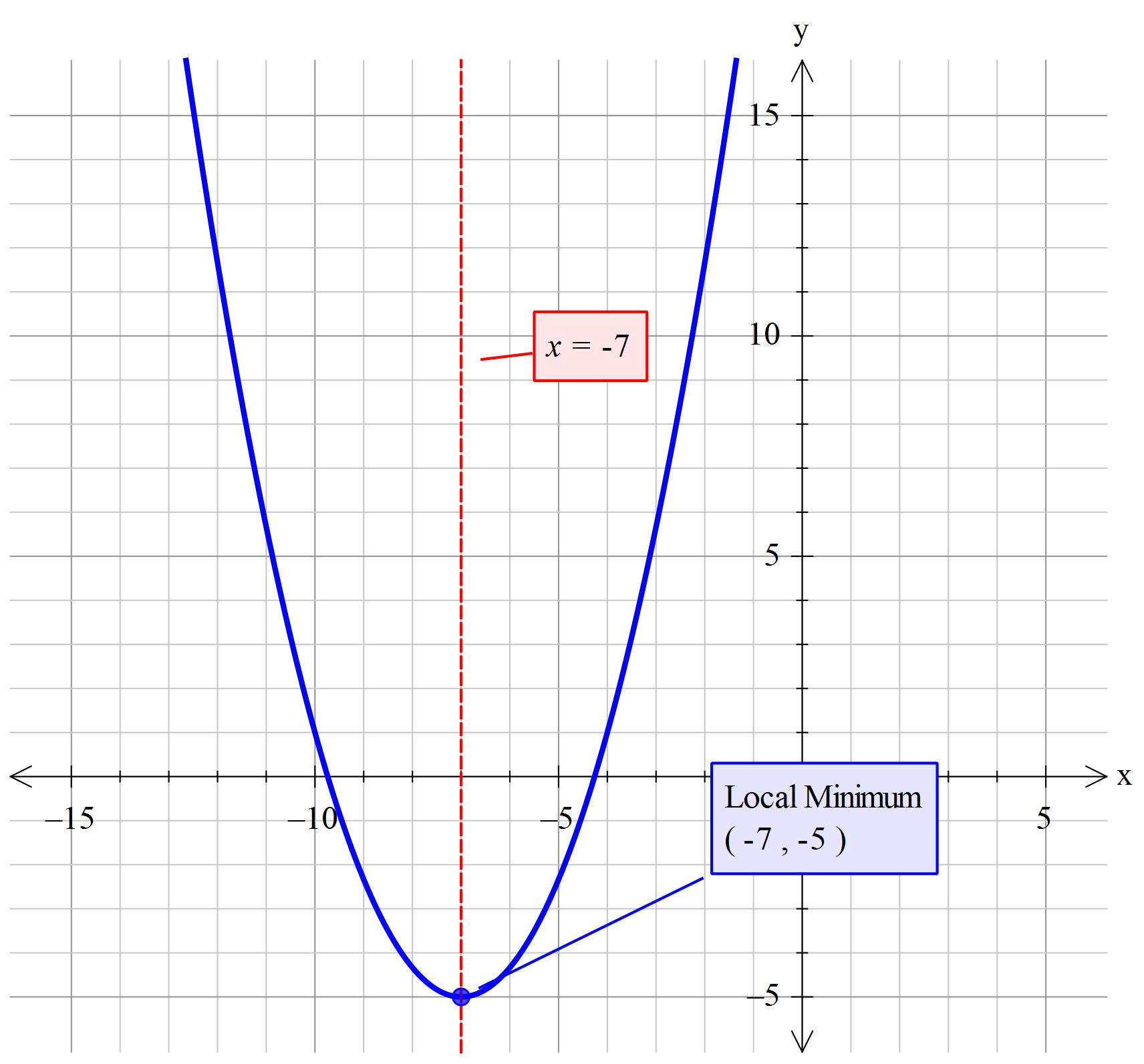



What Is The Axis Of Symmetry And Vertex For The Graph F X 2 3 X 7 2 5 Socratic
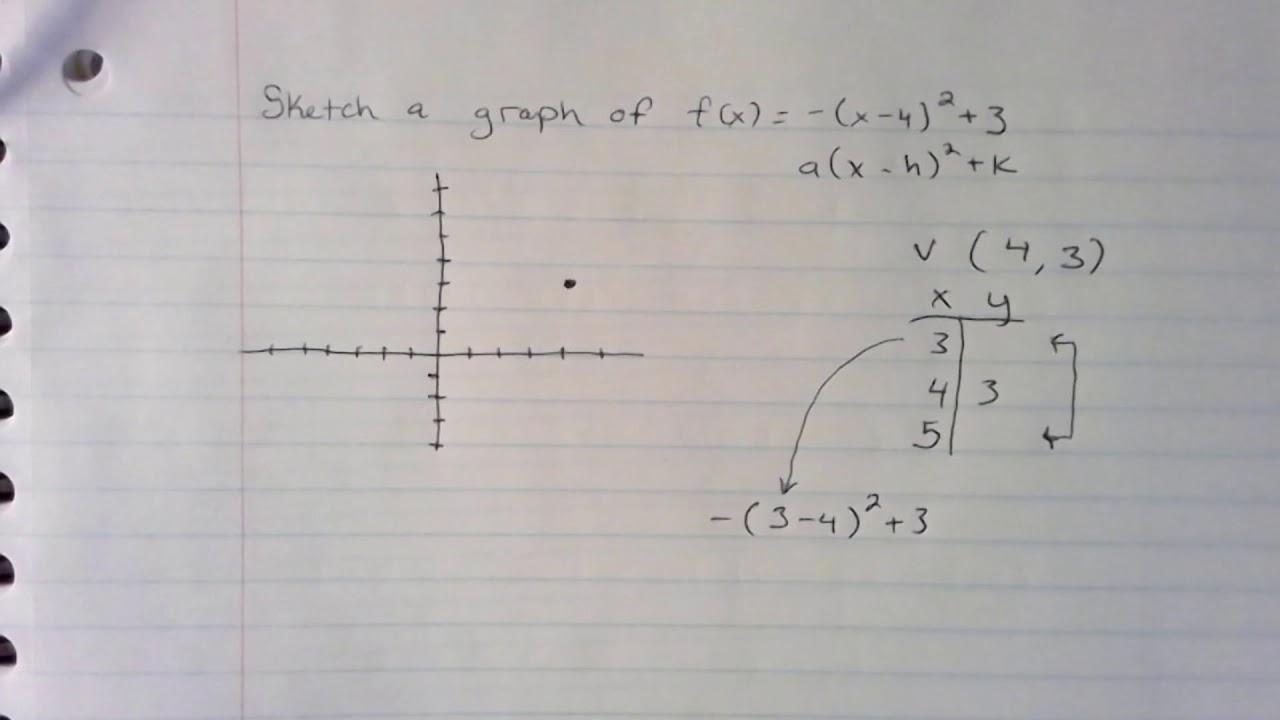



Graph F X X 4 2 3 Youtube
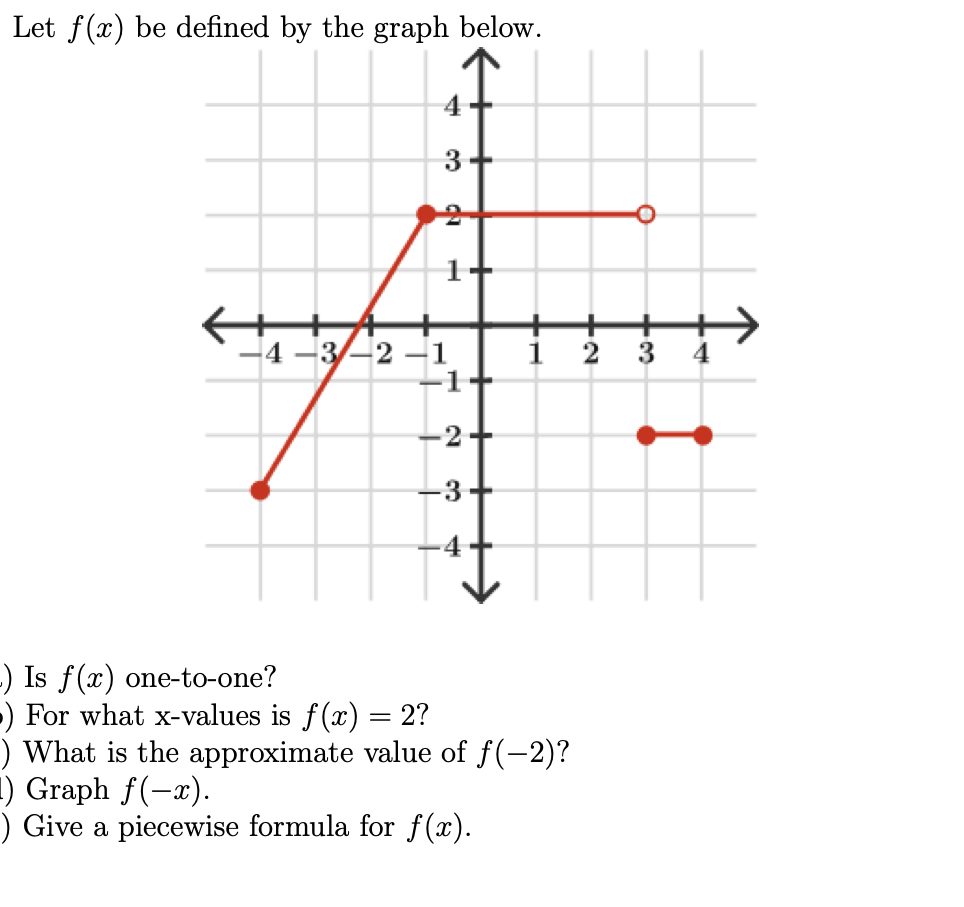



Solved Let F 2 Be Defined By The Graph Below 4 3 An 1 Chegg Com



Solved F X 3 X 2 2 F X 6x X 2 3 2 F X 18x 2 18 X 2 3 3 C Using The Graphs Off Andf Indicate Wheref Graph Down B Course Hero




Calculus Application Of Differentiation 18 Of 60 Graph F X 2x 3 3x 2 12x Using Derivatives Youtube
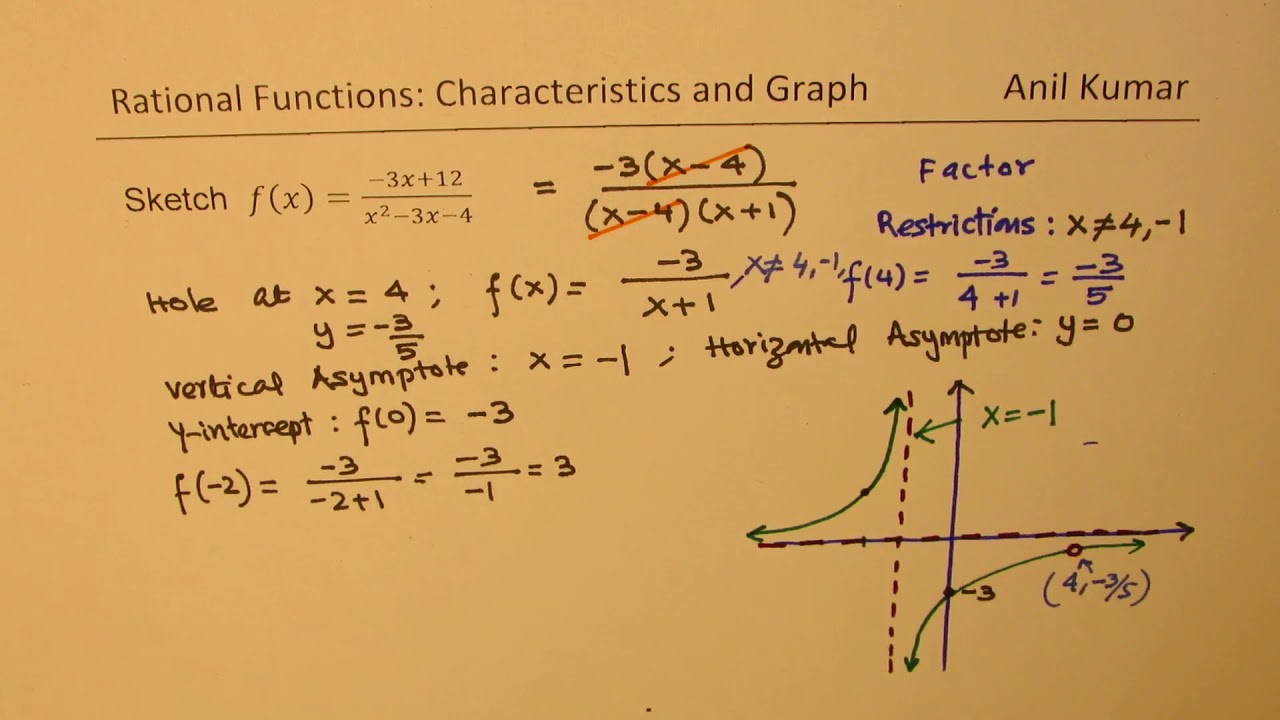



Sketch Graph 3x 12 X 2 3x 4 And Describe Behaviour Near Asymptotes Youtube




Power Functions F X X N N Is A Natural Number The Graphs Of Some Power Functions Are Given Below N Even N Odd Pdf Free Download
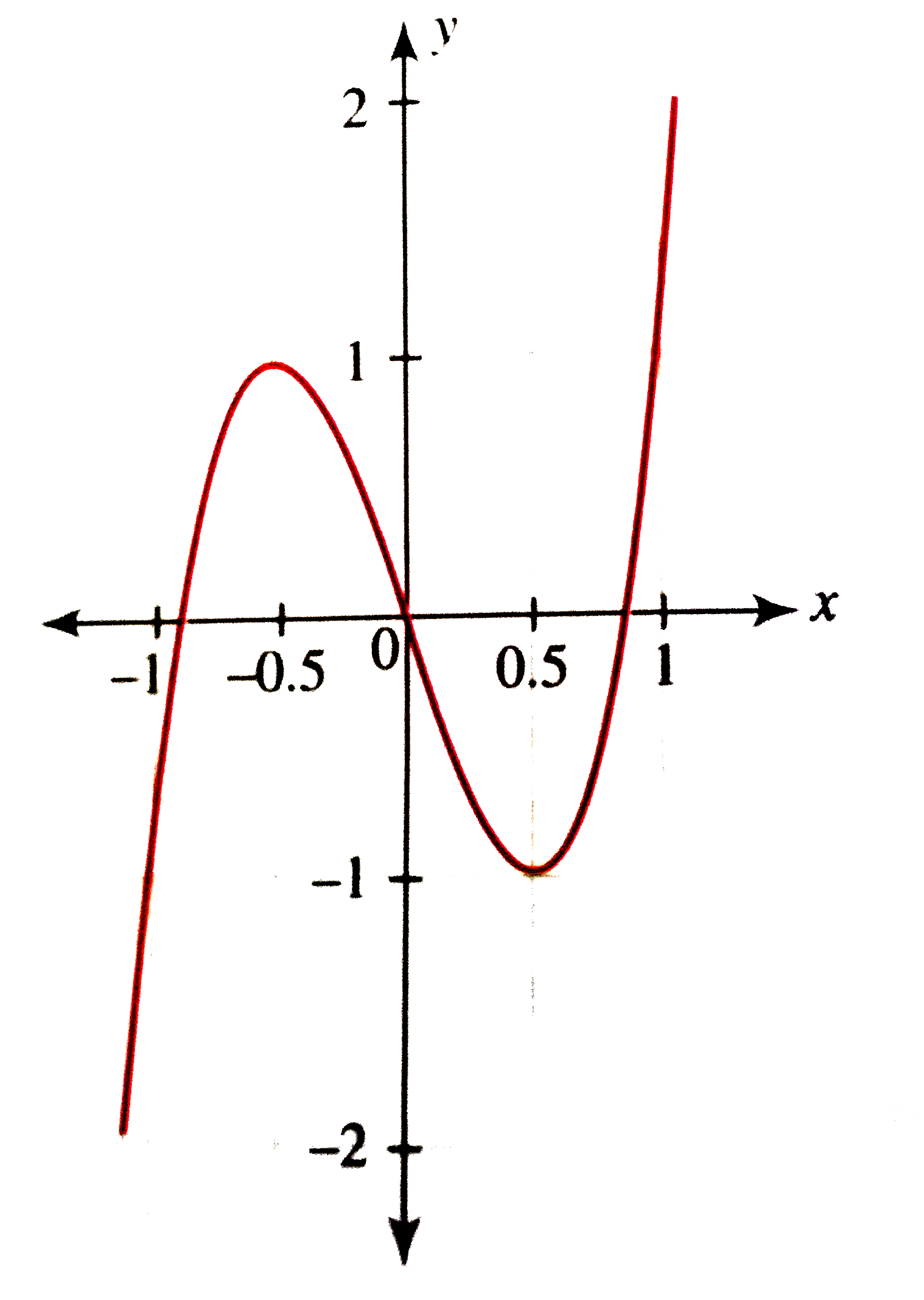



Draw The Graph Of F X 4x 3 3x And Hence Draw The Graph Of G
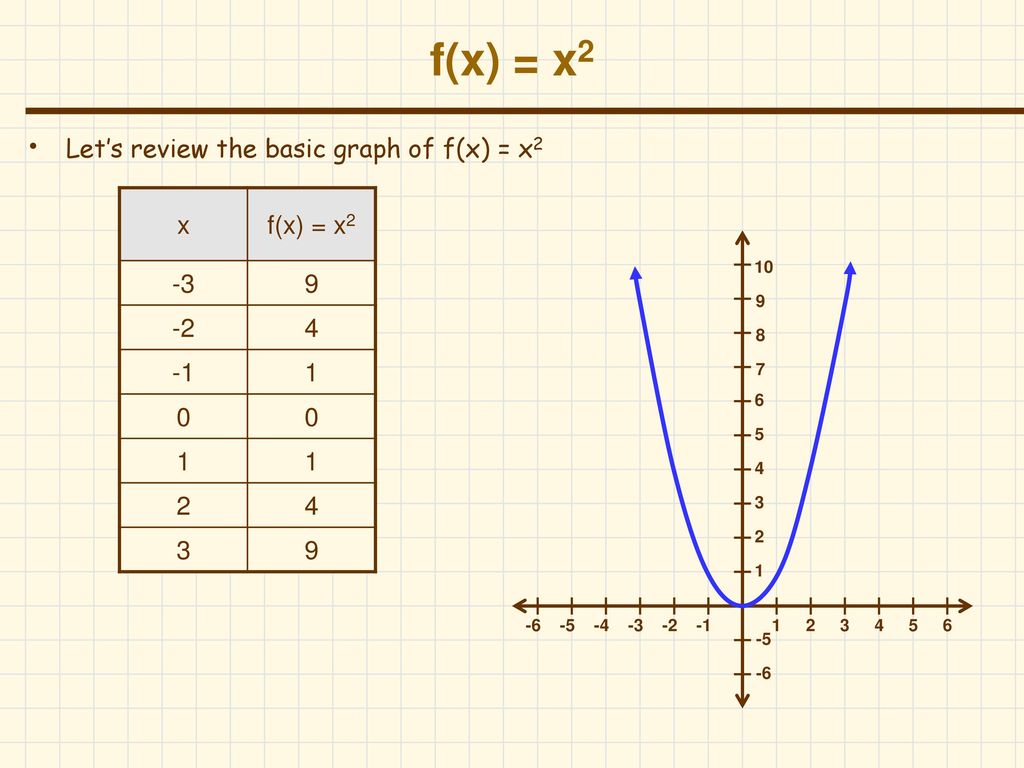



F X X2 Let S Review The Basic Graph Of F X X2 X F X X Ppt Download




Which Graph Models The Function F X 2 3 X Brainly Com
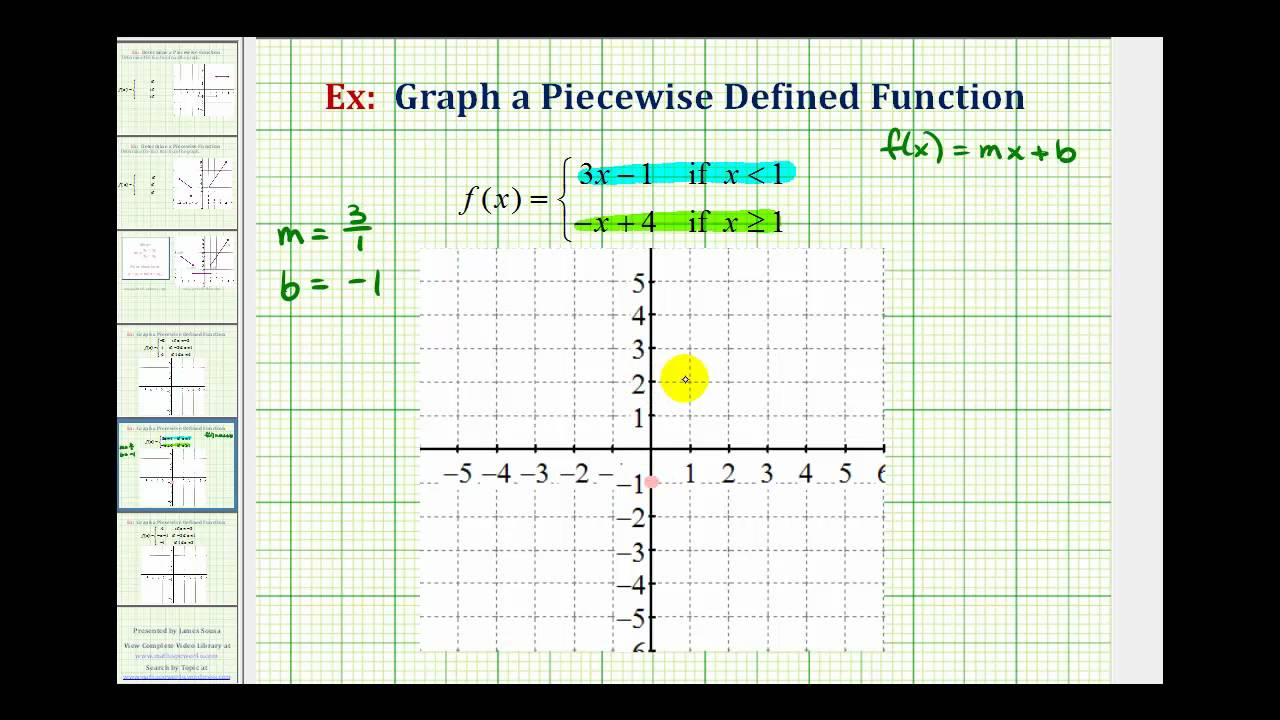



Piecewise Defined Functions College Algebra
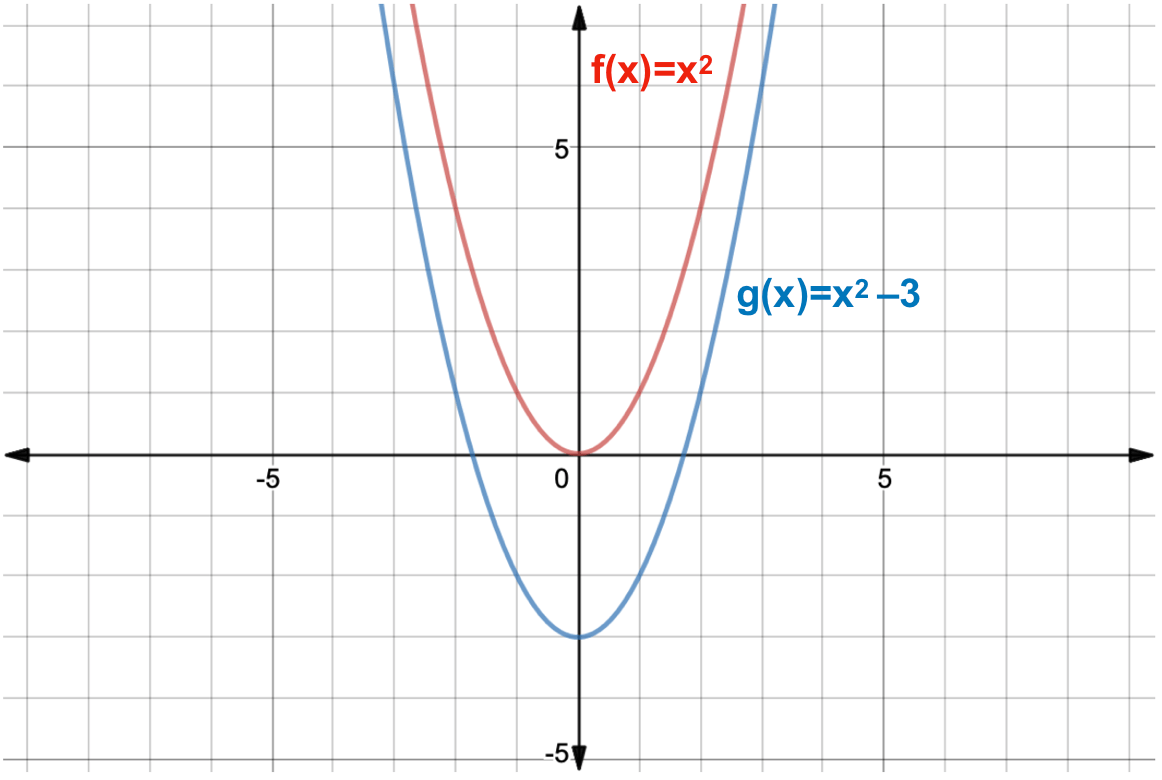



What Is A Function Transformation Expii




Graph The Function F X 3 2 X 4 2 3 Brainly Com




Equation Of Tangent Line F X X 3 X At X 2 Youtube
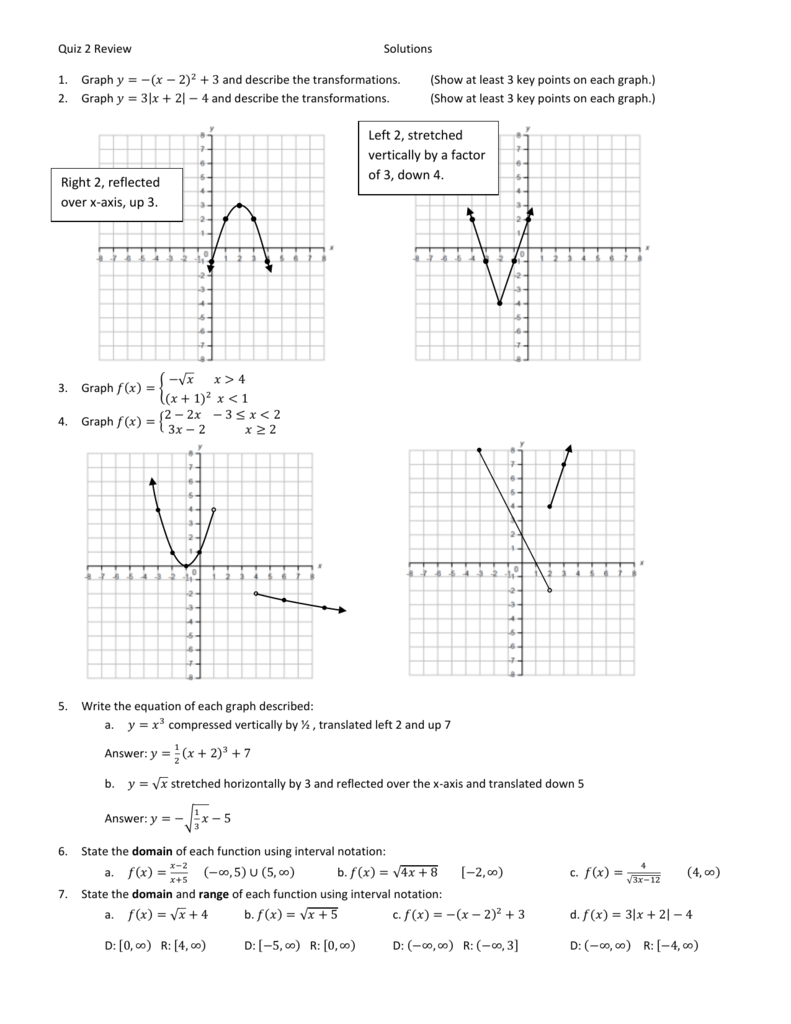



Calculus Chapter 2 Quiz Review Solutions
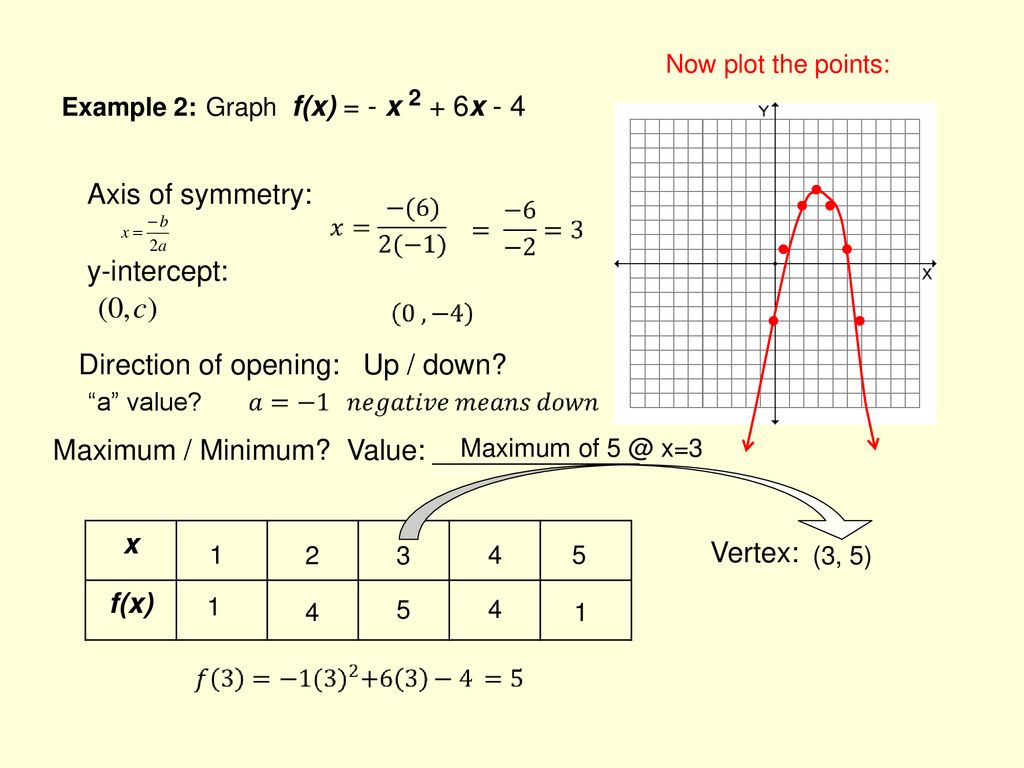



Quadratic Functions Graphing Ppt Download




Which Of The Following Represents Graph Of F X 1 2 X Brainly Com
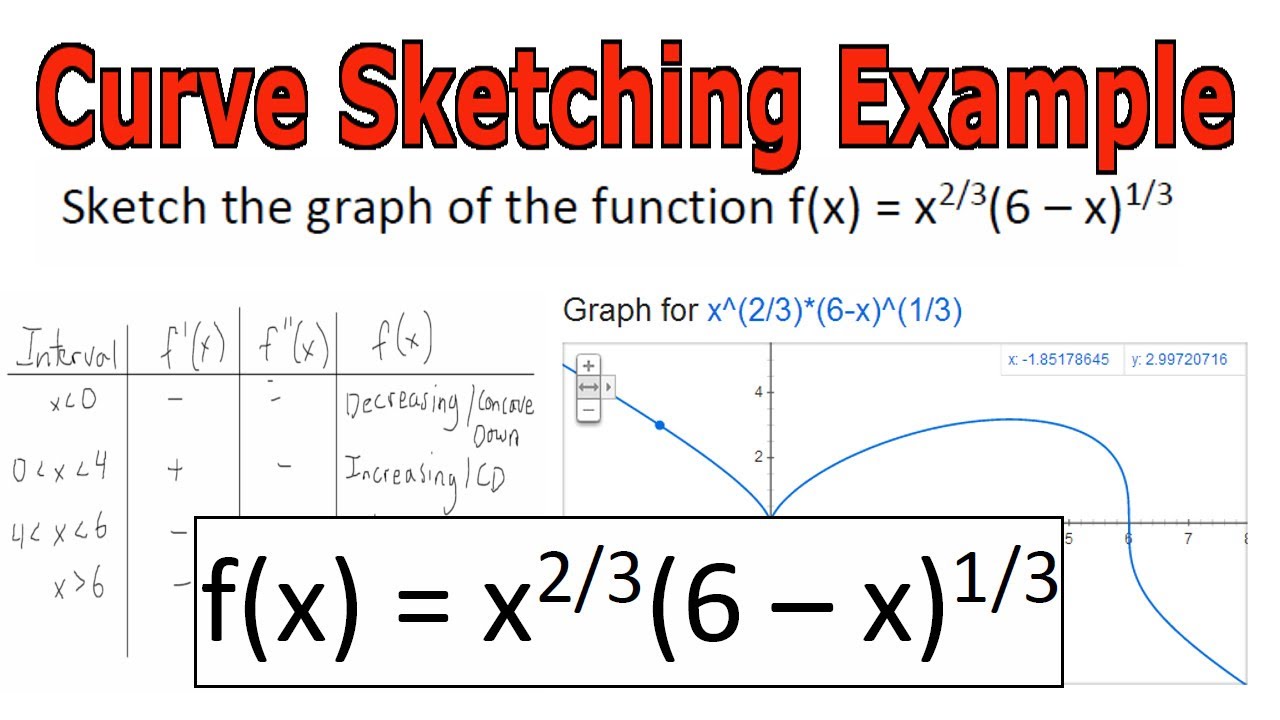



Curve Sketching Example Y X 2 3 6 X 1 3 Youtube
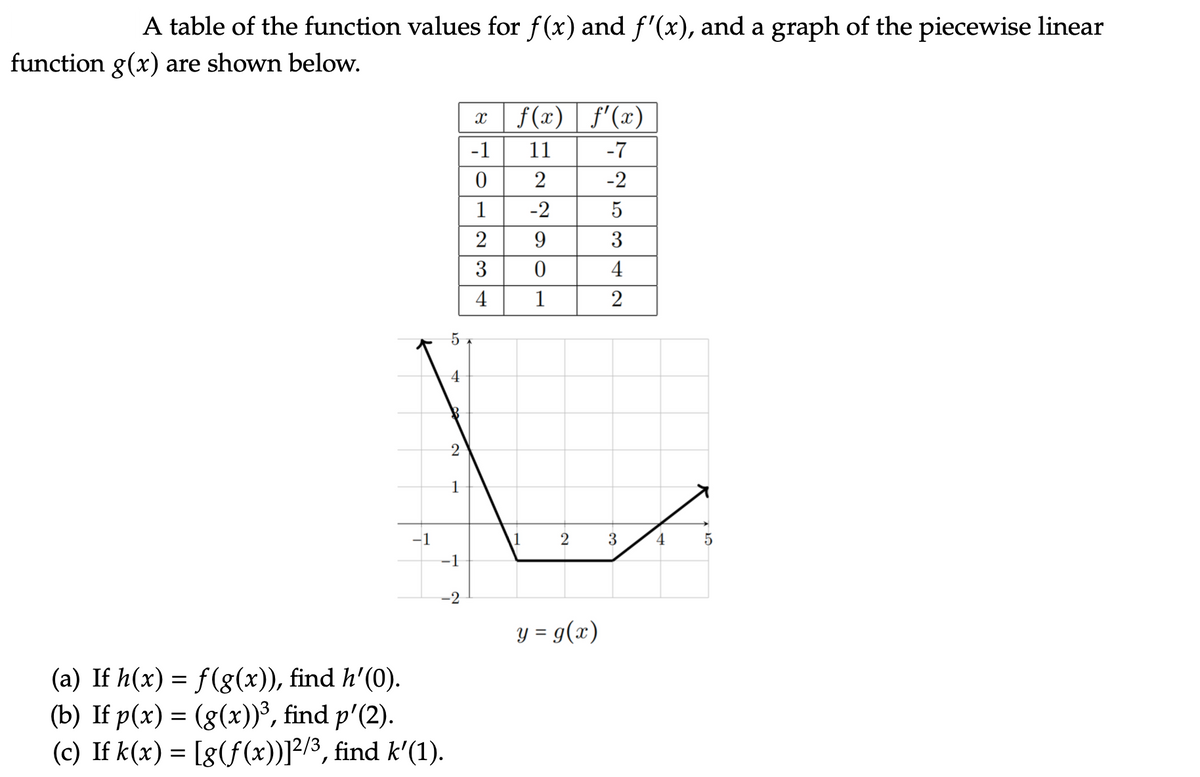



Answered A Table Of The Function Values For F X Bartleby




Which Graph Represents F X X 2 2 3 Brainly Com
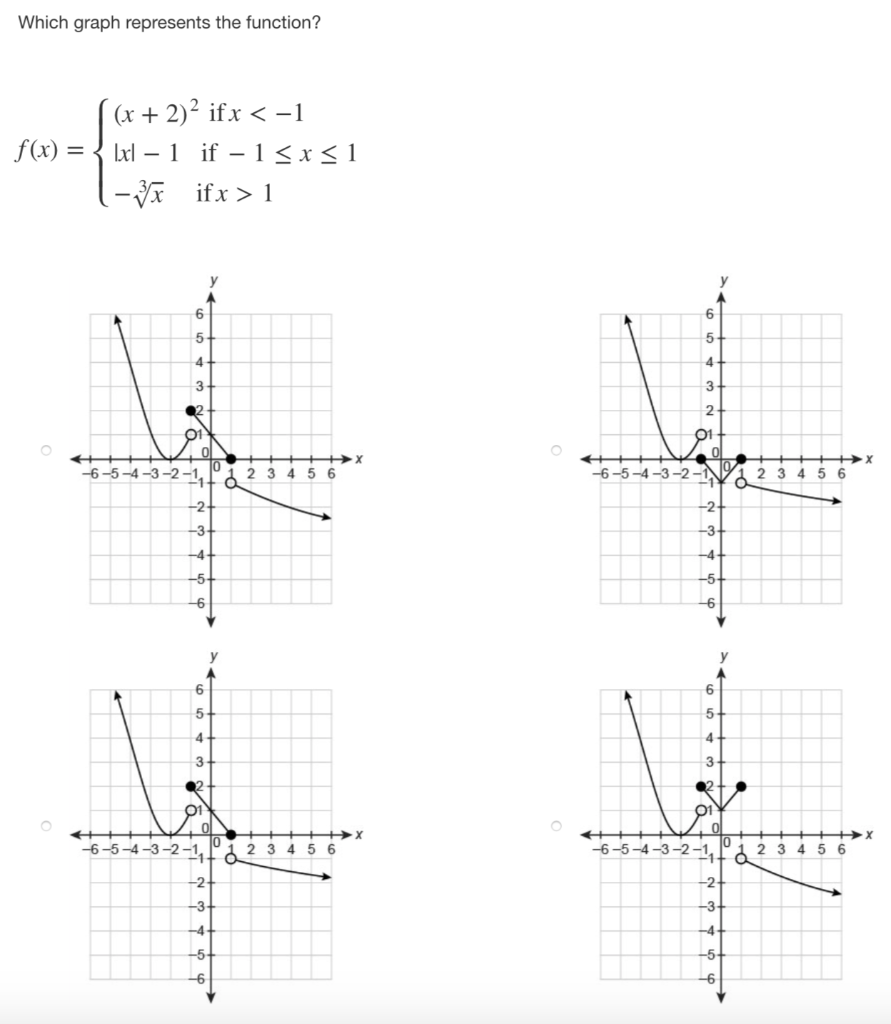



Which Graph Represents The Function F X X 2 2 Chegg Com




How To Graph A Quadratic Equation 10 Steps With Pictures



0 件のコメント:
コメントを投稿