If the CDF F is strictly increasing and continuous then (), ,, is the unique real number such that () = In such a case, this defines the inverse distribution function or quantile function Some distributions do not have a unique inverse (for example in the case where f X ( x ) = 0 {\displaystyle f_{X}(x)=0} for all a < x < b {\displaystyle aX ∈ R,x = −1 y ∈ R,y = 1 Explanation The denominator of f (x) cannot be zero as tis would make f (x) undefinedThe only function that is even and odd is f(x) = 0 Special Properties Adding The sum of two even functions is even;

Ex 5 1 8 Find Points Of Discontinuity F X X X If X 0
F x 0 if x is irrational
F x 0 if x is irrational-The tangent point x 0 As you move away from x 0, however, the approximation grows less accurate f(x) ≈ f(x 0) f (x 0)(x − x 0) Example 1 Let f(x) = 1ln x Then f (x) = x We'll use the base point x 0 = 1 because we can easily evaluate ln 1 = 0 Note also that f (x 0) = 1 1 = 1 Then the formula for linear approximation tells us that fIntegrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;




Use The Graph Of F X To Find The Intervals Where Chegg Com
Therefore you get f((x4) 4) which is f(x) as 44 is 0 Thus with the 4x, the x here would be substituted for (x4) which results with 4(x4) and if you expand that, you get 4x16 So f(x Example 3 Discuss the continuity of the function f given by 𝑓(𝑥) =𝑥 𝑎𝑡 𝑥 = 0 𝑓(𝑥) = 𝑥 𝑓(𝑥)= { (−𝑥, 𝑖𝑓 𝑥According to the composition law, we have lim x → 0 l n f ( x) = l n lim x → 0 f ( x) = l n c Because lim x → 0 g ( x) = d, we have lim x → 0 g ( x) l n f ( x) = lim x → 0 g ( x) ⋅ lim x → 0 l n f ( x) = d l n c Apply composition law again, we get
For example, the absolute value function given by f(x) = x is continuous at x = 0, but it is not differentiable there If h is positive, then the slope of the secant line from 0 to h is one, whereas if h is negative, then the slope of the secant line from 0 to h is negative one This can be seen graphically as a "kink" or a "cusp" in the graph at x = 0Is infinitely differentiable at x = 0, and has all derivatives zero there Consequently, the Taylor series of f (x) about x = 0 is identically zero However, f (x) is not the zero function, so does not equal its Taylor series around the origin Thus, f (x) is an example of a nonanalytic smooth functionLet us look at some details The Taylor series for f (x) at x = a in general can be found by f (x) = ∞ ∑ n=0 f (n)(a) n!
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Let x = c be the x coordinate of absolute max of f(x) on a, b (This point exists by the extreme value theorem) I will show that f(c) = 0 Since f(a) = 0 and c is the absolute max, f(c) ≥ 0 By Fermat's theorem, we know f ′ (c) = 0 Hence, we learn that f(c) = f ″ (c) ≥ 0X i j k dx 0 f dx 0 dy fydy x = (−f i −fy j k)dxdy , which is (11a) To get (11b) from (11a), , our surface is given by (12) F(x,y,z) = c, z = z(x,y) where the righthand equation is the result of solving F(x,y,z) = c for z in terms of the independent variables x and y We differentiate the lefthand equation in (12) with respect




Given F X X 2 4x Solve F X 0 By Factoring Youtube



Curve Sketching F X
We set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understandingFrom to Connect Dotted Dashed – Dashed — Fill in Fill out Show term Second graph g (x) Derivative Integral C Blue 1 Blue 2 Blue 3 Blue 4 Blue 5 Blue 6 Red 1 Red 2 Red 3 Red 4 Yellow 1 Yellow 2 Green 1 Green 2 Green 3 Green 4 Green 5 Green 6 Black Grey 1 Grey 2 Grey 3 Grey 4 White Orange Turquoise Violet 1 Violet 2 Violet 3 Violet 4In simple terms, that notation implies that f^1(x) is the Inverse Function to f(x) To make is a bit easier to wrtie, let's let g(x) be the inverse of f(x), in other words, g(x) = f^1(x) In terms of mappings, If D is the domain of f and R is the
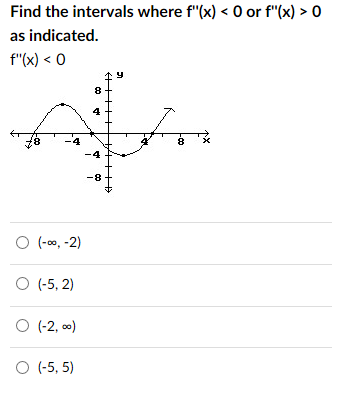



Find The Intervals Where F X 0 Or F X 0 As Chegg Com




Limits
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreYes they are The placement of the parentheses makes a difference For example with your graph above, when x = 4, f(x) = 0 and hence f(x) 2 =0 2 = 2 But f(x 2) = f(4 2) = f(2) = 2 In the second expression, since 4 2 is inside the parentheses you evaluate it first to get 2 and then use the table for y = f(x) to find f(2) Cheers, Ex 23, 5 Find the range of each of the following functionsf(x) = 2 – 3x, x ∈ R, x > 0Given that x > 0, Multiplying 3 both sides 3x > 0 × 3 3x > 0Multiplying 1 both sides – 1 × 3x < – 1 × 0 – 3x < 0Adding 2 both sides 2 – 3x < 2 0 (We need to make it in form



Approximate Solution To An Equation Newton S Method Or The Newton Raphson Method Use Of Newton S Method Example




How To Find The Equation Of A Tangent Line 8 Steps
# f(x)# is continuous at #x=a iff lim_(x rarr a)f(x)=f(a) # So, in order to prove that the function defined by # f(x) = xsin (1/x) # Is continuous at #x=0# we must show that # lim_(x rarr 0)xsin(1/x) = f(0) # This leads is to an immediate problem as #f(0)# is clearly undefined This is, however, not the end of the problem The derivative, f' (x), can be interpreted as "the slope of the tangent line" f' (x)> 0 means all tangent lines have positive slope are going up to the right Also "if x> 0, then f' (x)< 90" so for x positive, the derivative is negative which means tangent lines are going down to the right The short lines on each dot on the graph representClearly, h(x) = (mx b)(nx c) is a polynomial of degree 2 and h(x) has two roots The respective roots are when f(x) = 0 and g(x) = 0 This means the graph of h(x) crosses the xaxis at the same two points as f(x) and g(x) Thus, if there are points of tangency then they must occur at these common points on the xaxis




Ex 5 1 8 Find Points Of Discontinuity F X X X If X 0
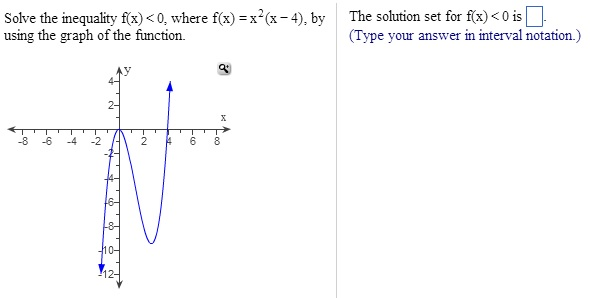



Solve The Inequality F X 0 Where F X Chegg Com
A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write "5x" instead of "5*x" The Integral Calculator has to detect these cases and insert the multiplication sign The parser is implemented in JavaScript, based on the Shuntingyard algorithm, and can run directly in the browserCBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Notes & Videos 531 Time Tables 18Mathf(x)=x/math Function is giving the absolute value of mathx/math whether mathx/math is positive or negative See the y axis of graph which is mathf(x)/math against mathx/math, as x axis It shows y axis values or mathf(x



15 10 Limit Of A Piece Wise Function Graphing Calculator By Mathlab User Manual




The Graph Of A Function F Is Shown Below Find One Value Of X For Which F X 4 And Find F 2 Solved
Explanation Both 1 x 1 and 1 x −1 are continuous at 0, so both e 1 x1 and e 1 x−1 are continuous at 0 Because e 1 x−1 ≠ 0 at x = 0, the quotient e 1 x1 e 1 x−1 is also continuous at 0 In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);In this *improvised* video, I show that if is a function such that f(xy) = f(x)f(y) and f'(0) exists, then f must either be e^(cx) or the zero function It'




Solve An Absolute Value Equation College Algebra



Graphing The Basic Functions
The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6 You must remember that f(x)=y (value on the yaxis) Well, you have an xaxis, and you look at where it intersects with the yaxis At this point, y=0, and x=0 As long as you move along the xaxis (to the left or to the right), the yvalue will stay 0The expression f(0) represents the yintercept on the graph of f(x) The yintercept of a graph is the point where the graph crosses the yaxis This occurs where x is equal to 0 Therefore, if we plug x = 0 into a function, denoted f(0), the result will be the yintercept
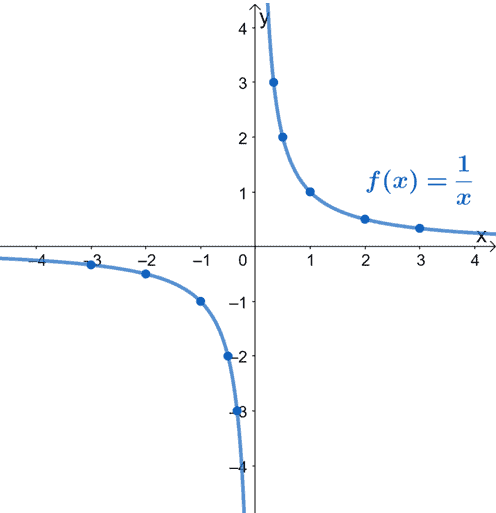



Reciprocal Function Properties Graph And Examples




14 2 What Values Of X Does F X 0 Youtube
F/X Directed by Robert Mandel With Bryan Brown, Brian Dennehy, Diane Venora, Cliff De Young A movie special effects man is hired to fake a reallife mob killing for a witness protection plan, but finds his own life in danger 1 Answer Wataru The Taylor series of f (x) = cosx at x = 0 is f (x) = ∞ ∑ n=0( −1)n x2n (2n)! real analysis Show that $f$ is the zero function if $f''(x)=f(x)$ and $f(0)=f'(0)=0$ Mathematics Stack Exchange Suppose that $f''(x)=f(x)$ for all real numbers $x$, and that $f(0)=f'(0)=0$ Show that $f$ is the zero function I know



Biomath Power Functions




How To Find The Equation Of A Tangent Line 8 Steps
Implying $F(F(x))x\gt 0,$ for all $x\in\mathbb{R}$ The case $f(x)\lt 0$ is treated similarly Thus for no real $x,$ $F(F(x))=x$ Solution 4 This is a simplified paraphrase of the previous proof, with aGraph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the(x − a)n Let us find the Taylor series for f (x) = cosx at x = 0



Search Q Point Of Inflection Tbm Isch




Quadratic Example For What Values Of X Is F X Greater Than 0 Youtube
Integrate 1/(cos(x)2) from 0 to 2pi;Find the Intervals in Which F(X) = Sin X − Cos X, Where 0 < X < 2π is Increasing Or Decreasing ?Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect square



Inflection Points




Extrema Of A Function
Let f(x) = {(1 cos 4x)/x2, if x < 0 and a, if x = 0 and √x/(√(16 √x) 4), if x > 0} If f(x) is continuous at x = 0, determine the value of aView more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator LearnThe sum of two odd functions is odd;




Match The Conditions F X Less Than 0 And F X Less Than 0 With One Of The Graphs In The Figure Study Com
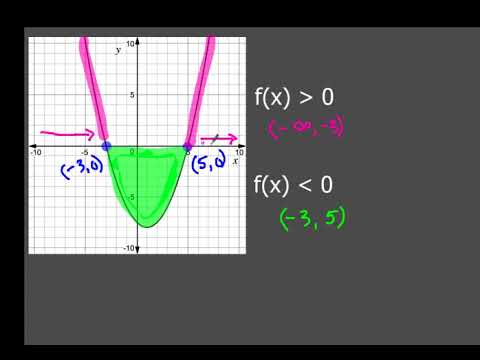



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube
Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations context Let f be a realvalued function on R satisfying f(xy)=f(x)f(y) for all x,y in R If f is continuous at some p in R, prove that f is continuous at every point of R Proof Suppose f(x) is continuous at p in R Let p in R and e>0 Since f(x) is continuous at p we can say that for all e>0Because f is continues, if f (a)> 0 or f (a) < 0 then f = ∣f ∣ or −∣f ∣ in the neighborhood of a, respectively, and so f is differentiable at a If f (a) = 0 then ∣f (a)∣′ = 0, because ∣f ∣ is Proving that a positive derivative means the function is smaller "to the



Solving Polynomial Inequalities By Graphing
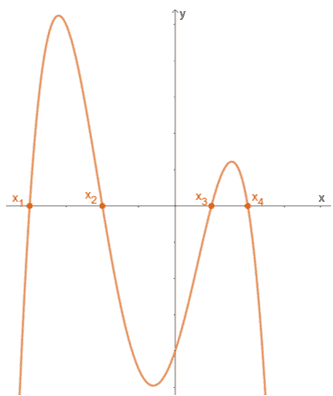



Zeros Of A Function Explanation And Examples
In other words, we are looking for the xintercept, since y=0 for all xintercepts So we substitute 0 in for f(x) and we get Now we solve for x Add 12 to both sides Divide both sides by 3 This will isolate x So if we let x=4 we should get f(x)=0, in other words, f(4)=0 So lets verify this Check Plug in x=4 works This verifies our answerStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange The function f(x)=0 has both It's graph is simply a horizontal line on the X axis, and is both symmetrical about the Y axis, and also about the origin Also, if one were to do the algebra, f(x) would equal 0, which is the same as f(x), but could also be considered the opposite of f(x), as 1 x 0 = 0



Biomath Power Functions



Functions Inverse And Composite Functions
A) If f'(x) >0 on an interval, then f is increasing on that interval b) If f'(x) 0 on an interval, then f is concave upward on that interval d) If f''(x)Note If f takes its values in a ring (in particular for real or complexvalued f ), there is a risk of confusion, as f n could also stand for the nfold product of f, eg f 2 (x) = f(x) f(x) For trigonometric functions, usually the latter is meant, at least for positive exponents We are approximating an area from a to b with a=0 and b=5, n=5, right endpoints and f(x)=25x^2 (For comparison, we'll do the same problem, but use left endpoints after we finish this) We need Delta x=(ba)/n Deltax is both the base of each rectangle and the distance between the endpoints For this problems Deltax=(50)/5=1 Now, find the endpoints
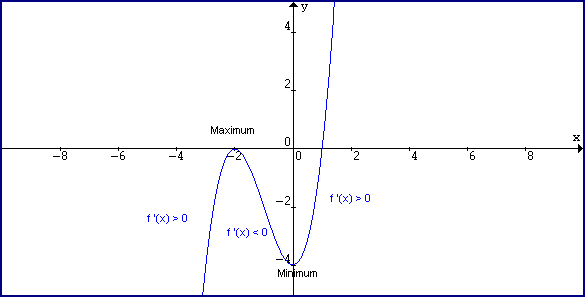



Derivative And Tangent Line



The Function F Is Defined By F X 1 X X 0 1 X 0 X 1 X 0 Draw The Graph Of F X Sarthaks Econnect Largest Online Education Community
Summary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functionsExample 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the firstThe Function which squares a number and adds on a 3, can be written as f (x) = x2 5 The same notion may also be used to show how a function affects particular values Example f (4) = 4 2 5 =21, f (10) = (10) 2 5 = 105 or alternatively f x → x2 5 The phrase "y is a function of x" means that the value of y depends upon the value of



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf
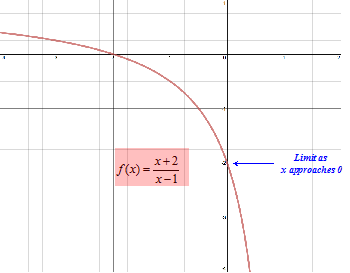



Limits Introduction And One Sided Limits
The sum of an even and odd function is neither even nor odd (unless one function is zero) Multiplying The product of two even functions is an even function
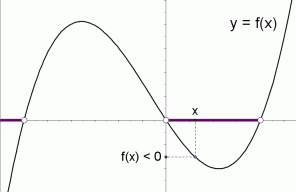



Graphical Interpretation Of Sentences Like F X 0 And F X 0



Critical Points
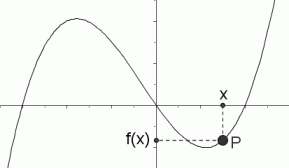



Graphical Interpretation Of Sentences Like F X 0 And F X 0




If F X E 1 X 1 Ifx 0ifx 0 Find Whether F Is Continuous At X 0



3



What Is The Maclaurin Series X 0 For F X Sin 2x Socratic



Math Scene Equations Iii Lesson 3 Quadratic Equations




Use The Graph Of F X To Find The Intervals Where Chegg Com
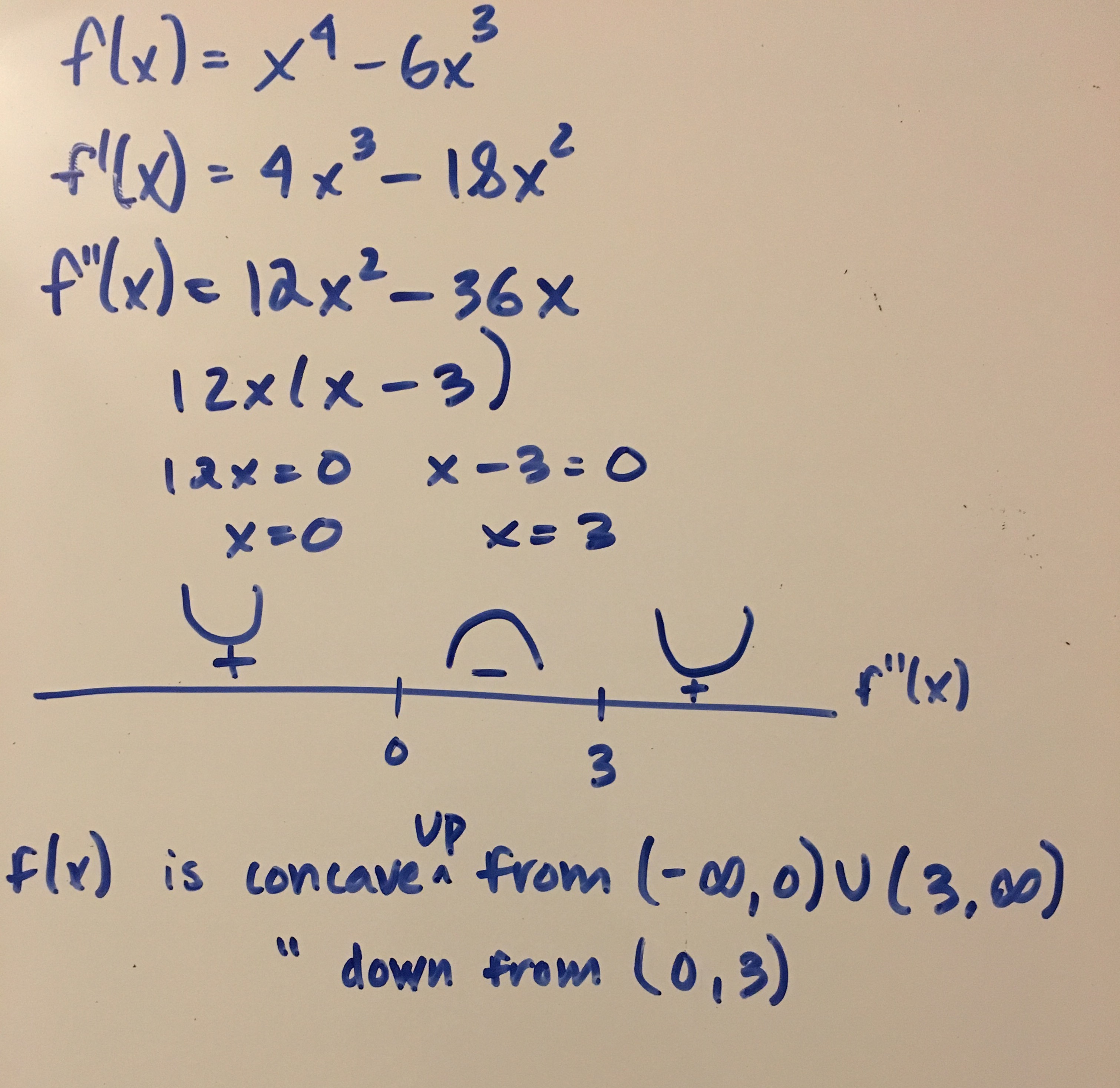



How Do You Ise Interval Notation Indicate Where F X Is Concave Up And Concave Down For F X X 4 6x 3 Socratic



4 1 Extreme Values Of Functions Mathematics Libretexts
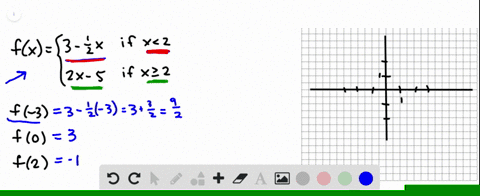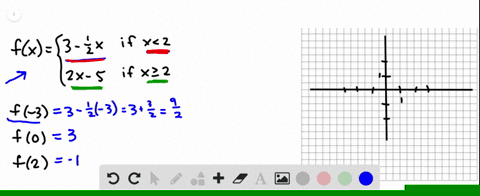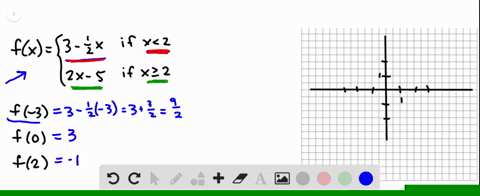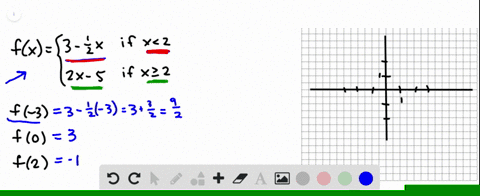



Solved Given The Following Graph Cdot Evaluate F 0 Cdot Solve For F X 3




Is The Function F Defined By F X X If X 1 Continuous At X 0 At X 1 At X 2




4 3 Connecting F And F With The Graph Of F Magic Light Calculus



What Does F 0 Represent On The Graph Of F X Quora
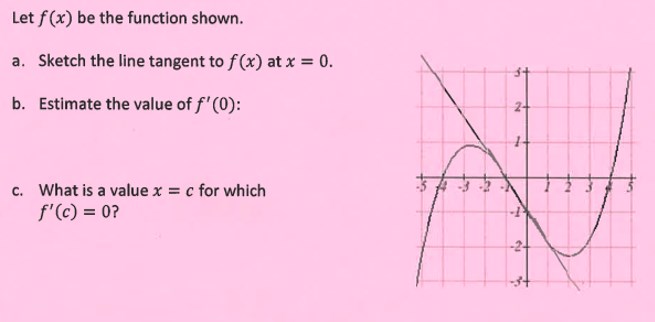



Estimate The Value Of F 0 Additionally What Is A Value X C For Which F C 0 Part A Is Already Done Socratic




Graphing The Basic Functions




Find Limits Of Composition In The Graph Of F Mathematics Stack Exchange



Inflection Points



Calc 1 F X 0 If X 0 What Does This Mean Physics Forums



Solution Use The Graph Of The Function To Estimate A F 2 B F 4 C All X Such That F X 0 I Can 39 T Show The Graph On Here It Won 39 T Copy And




Example 2 Examine Whether F X X2 Is Continuous At X 0




Relu Derivative In Backpropagation Stack Overflow



Applications Of Differentiation The Graph Of A Function And Its Derivatives Extreme Points Of A Function Local Or Relative Maximum And Local Minimum Of A Function The First Derivative Test The Second




Question Video Finding The Solution Set Of A Quadratic Equation Graphically Nagwa




At What Values Of X Does F X 0 Brainly Com




Justification With The Intermediate Value Theorem Table Video Khan Academy




Is Modulus Function Differentiable Quora



Http Smacmathapcalculus Weebly Com Uploads 1 9 2 5 Apc Hw 4 6 Key Pdf



Mathematics Calculus



Sage Calculus Tutorial Continuity



Sage Calculus Tutorial Differentiability




7 Find The Fourier Series Of The Given Function A F X 1 P X P B F X 0 2 Ke 0 X 1 1 X 0 1 1 X 0 F X




The Derivative Function



Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf
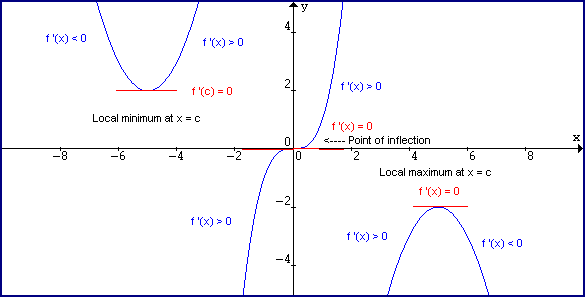



Derivative And Tangent Line
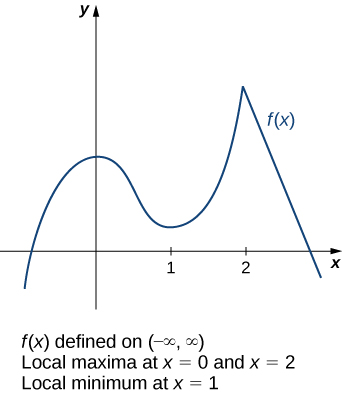



4 1 Extreme Values Of Functions Mathematics Libretexts
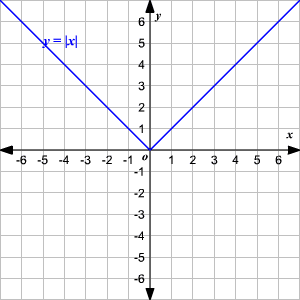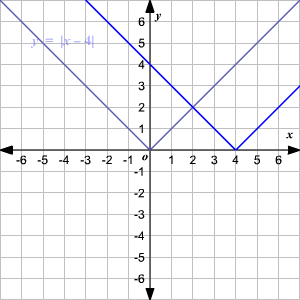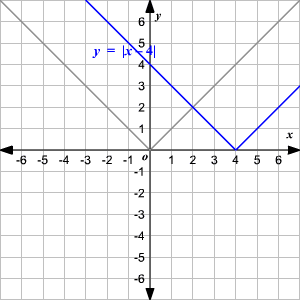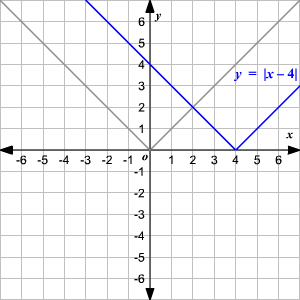



Absolute Value Functions




The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com




Introduction To Limits In Calculus




How To Use Graph To Determine Where F X 0 And F X 0 Mathematics Stack Exchange




If F X 2f 1 X 3x X 0 And S X In R F X F X Then S 1 Is An Empty Set 2 Contains Exactly One Element 3 Contains Exactly Two Elements 4 Contains More Than Two



Content Newton S Method



Solve F X 0 X



Www Ebnet Org Cms Lib Nj Centricity Domain 816 17 18 chapter 5 period 3 answer key Pdf




1 Concave Upwards G X 0 2 Concave Downwards G X 0 Negative Slope Y G X Positive Slope Zero Slope Ppt Download




Inflection Points Points Of Inflection Iitutor
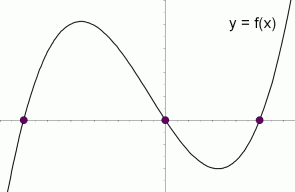



Graphical Interpretation Of Sentences Like F X 0 And F X 0
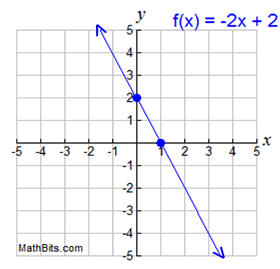



Features Of Function Graphs Mathbitsnotebook A1 Ccss Math



What Does F X X Mean Quora



Graphing A Function Using The First Derivative Graph Math100 Mirka



Sat Math Graph Example 2 Sat Math Forbest Academy



1




Example 4 Show F X X3 3 1 Is Not Continuous At X 0
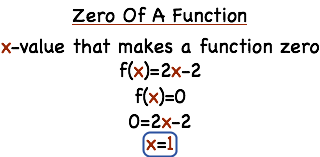



What S The Zero Of A Function Printable Summary Virtual Nerd




Solving Fx 0 And Fx Gx Youtube
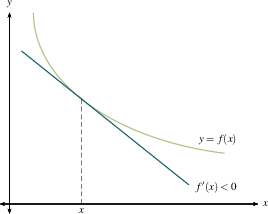



F Vs F
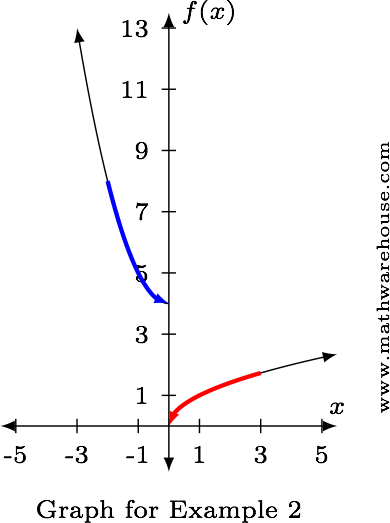



Limits Of Piecewise Defined Functions How To Calculate Examples Practice Problems Pictures



Business Calculus




Turning Points And Nature Iitutor




Fourier Series Periodic Functions A Function Fx Is




Theorem For Limits Of Composite Functions Video Khan Academy
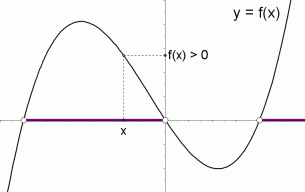



Graphical Interpretation Of Sentences Like F X 0 And F X 0




Use The Given Graph Of F X To Find The Intervals On Chegg Com
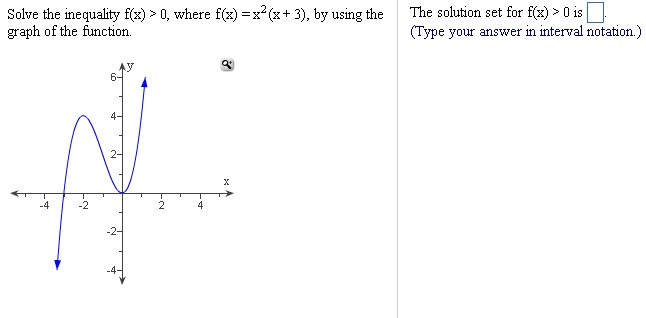



Solve The Inequality F X 0 Where F X X 2 X Chegg Com
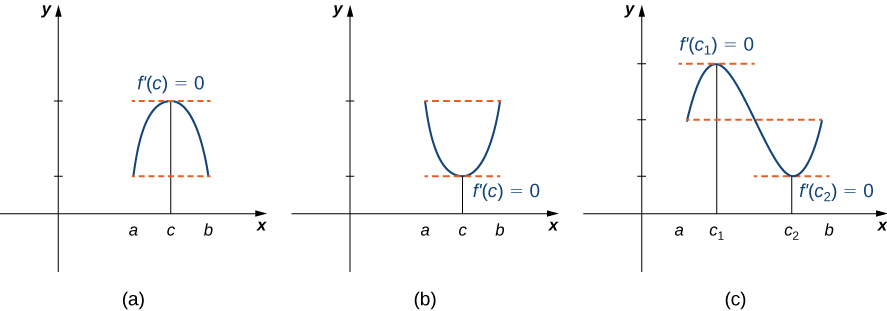



4 4 The Mean Value Theorem Calculus Volume 1
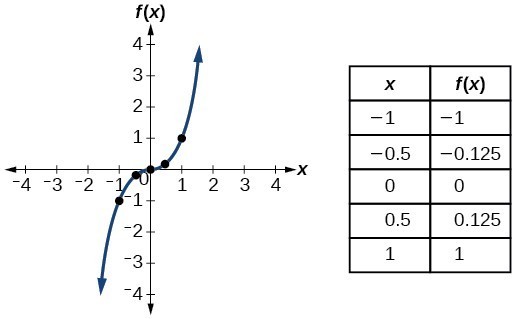



11 1 Toolkit Functions Hunter College Math101




Funciones F X 0 F X 0 Geogebra



Solving Polynomial Inequalities By Graphing




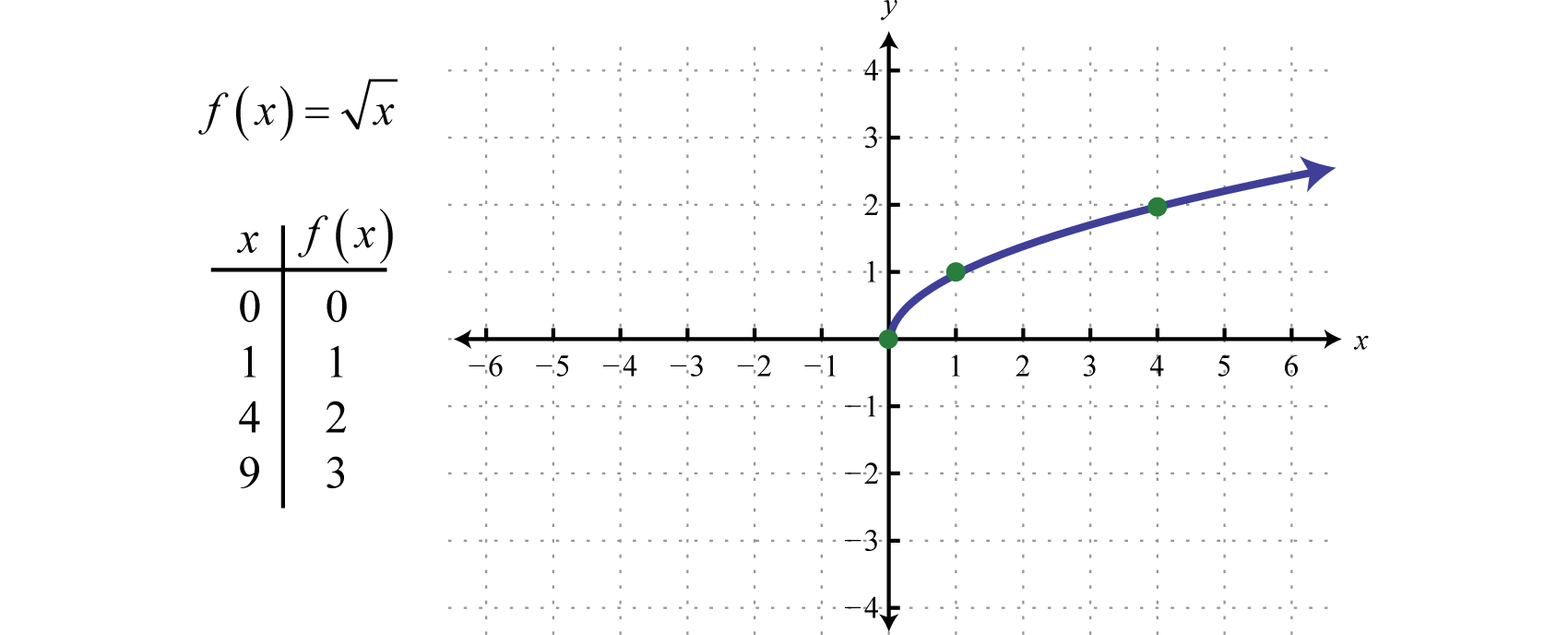
Graphing Square Root Functions




Use The Graph Of F To Determine Where A F X 0 And Chegg Com
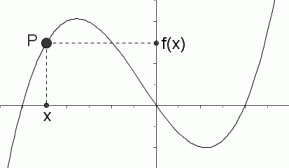



Graphical Interpretation Of Sentences Like F X 0 And F X 0




Zero Function Wikidata



F X 0




Analyzing Graphs Flashcards Quizlet



0 件のコメント:
コメントを投稿